题目内容
19.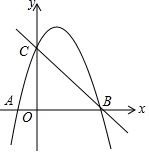 如图所示在平面直角坐标系中.抛物线y=-x2+bx+c与x轴交于A、B两点(A在B的左侧),与y轴交于C点,直线y=-x+3经过B,C 两点.
如图所示在平面直角坐标系中.抛物线y=-x2+bx+c与x轴交于A、B两点(A在B的左侧),与y轴交于C点,直线y=-x+3经过B,C 两点.(1)求该抛物线的解析式;
(2)在直线BC上方的抛物线上是否存在一动点P.使四边形PCOB的面积最大?如果存在,求出最大面积,并指出此时P点的坐标;如果不存在,请简要说明理由;
(3)若点E是抛物线对称轴上一动点.把OE绕点E旋转90°,点O的对应点为G,若点G恰好落在抛物线上,则称这样的点E为“好点”,请直接写出所有“好点”E的坐标.
分析 (1)求出B、C两点坐标,利用待定系数法即可解决问题.
(2)存在.设P(m,-m2+2m+3),由题意S四边形PCOB=S△PCO+S△OPB=$\frac{1}{2}$×3×m+$\frac{1}{2}$×3×(-m2+2m+3)=-$\frac{3}{2}$(m-$\frac{3}{2}$)2+$\frac{63}{8}$,由此利用二次函数的性质即可解决问题.
(3)①如图2中,设对称轴与x轴交于点H,设E(1,m).作GD⊥EH于D.由△OEH≌△EGD,可得DE=OH=1,DG=EH=m,则G(m+1,m-1),把G(m+1,m-1)代入y=-x2+2x+3得到m-1=-(m+1)2+2(m+1)+3,解方程即可解决问题.②如图3中,设对称轴与x轴交于点H,设E(1,m).作GD⊥EH于D.同法可求.
解答 解:(1)对于直线y=-x+3令x=0得到y=3,令y=0得到x=3,
∴B(3,0),C(0,3),把B(3,0),C(0,3)代入y=-x2+bx+c得到$\left\{\begin{array}{l}{c=3}\\{-9+3b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$,
∴抛物线的解析式为y=-x2+2x+3.
(2)存在.理由如下:
如图1中,设P(m,-m2+2m+3),
∴S四边形PCOB=S△PCO+S△OPB=$\frac{1}{2}$×3×m+$\frac{1}{2}$×3×(-m2+2m+3)=-$\frac{3}{2}$(m-$\frac{3}{2}$)2+$\frac{63}{8}$,
∵-$\frac{3}{2}$<0,
∴m=$\frac{3}{2}$时,四边形ABPC的面积最大,此时p($\frac{3}{2}$,$\frac{15}{4}$).
(3)①如图2中,设对称轴与x轴交于点H,设E(1,m).作GD⊥EH于D.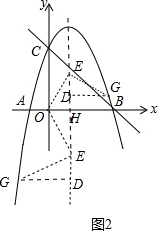
由△OEH≌△EGD,可得DE=OH=1,DG=EH=m,则G(m+1,m-1),
把G(m+1,m-1)代入y=-x2+2x+3得到m-1=-(m+1)2+2(m+1)+3,解得m=$\frac{-1±\sqrt{21}}{2}$,
∴点E坐标为(1,$\frac{-1+\sqrt{21}}{2}$)或(1,$\frac{-1-\sqrt{21}}{2}$).
②如图3中,设对称轴与x轴交于点H,设E(1,m).作GD⊥EH于D.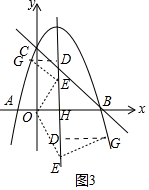
同法可得G(1-m,m+1),把G(1-m,m+1)代入y=-x2+2x+3得到m+1=-(1-m)2+2(1-m)+3,解得m=$\frac{-1±\sqrt{13}}{2}$,
∴点E的坐标为(1,$\frac{-1+\sqrt{13}}{2}$)或(1,$\frac{-1-\sqrt{13}}{2}$).
点评 本题考查二次函数综合题、一次函数的性质、待定系数法、四边形的面积、等腰直角三角形的性质、全等三角形的判定和性质等知识,解题的关键是学会构建二次函数解决最值问题,学会用分类讨论的思想思考问题,属于中考压轴题.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案圆圆同学的求解过程如下:
7x-2≤9x+3
7x-9x≤3-2
-2x≤1
x≤-$\frac{1}{2}$
请你判断圆圆的求解过程是否正确,若不正确,请你给出正确的求解过程.
| A. | -1 | B. | π | C. | 0 | D. | $\sqrt{9}$ |
 如图,一个可以自由转动的转盘被等分成6个扇形区域,并涂上了相应的颜色,转动转盘,转盘停止后,指针指向黄色区域的概率是$\frac{1}{6}$.
如图,一个可以自由转动的转盘被等分成6个扇形区域,并涂上了相应的颜色,转动转盘,转盘停止后,指针指向黄色区域的概率是$\frac{1}{6}$.
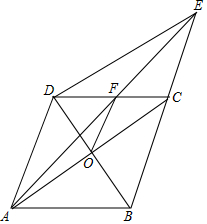 已知:如图,?ABCD中,对角线AC,BD相交于点O,延长BC至E,使CE=BC,连接AE交CD于点F.
已知:如图,?ABCD中,对角线AC,BD相交于点O,延长BC至E,使CE=BC,连接AE交CD于点F.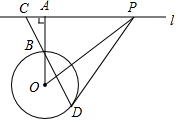 如图,直线l与⊙O相离,过点O作OA⊥l,垂足为A,OA交⊙O于点B,点C在直线l上,连接CB并延长交⊙O于点D,在直线l上另取一点P,使∠PCD=∠PDC.
如图,直线l与⊙O相离,过点O作OA⊥l,垂足为A,OA交⊙O于点B,点C在直线l上,连接CB并延长交⊙O于点D,在直线l上另取一点P,使∠PCD=∠PDC.