题目内容
8．
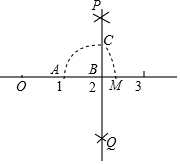如图，数轴上点A、B对应的数分别是1，2，过点B作PQ⊥AB，以点B为圆心，AB长为半径作圆弧，交PQ于点C，以原点O为圆心，OC长为半径画弧，交数轴于点M，当点M在点B的右侧时，点M对应的数是$\sqrt{5}$．
分析 先依据勾股定理可求得OC的长，从而得到OM的长，于是可得到点M对应的数．
解答 解：由题意得可知：OB=2，BC=1，
依据勾股定理可知：OC=$\sqrt{O{B}^{2}+B{C}^{2}}$=$\sqrt{5}$．
∴OM=$\sqrt{5}$．
故答案为：$\sqrt{5}$．
点评 本题主要考查的是实数与数轴，熟练掌握相关知识是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
18．函数y=$\frac{3}{x-1}$中，自变量x的取值范围是（ ）
| A． | x＞1 | B． | x≠3 | C． | x≠1 | D． | x≠0 |
如图，h与b相交于O点，若∠1=30°，则∠2的度数是150°，∠3的度数是30°．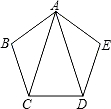
如图，在正五边形ABCDE中，AC、AD为对角线，则∠CAD的大小为36°．
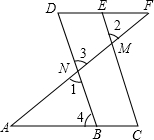在横线上填出正确的结论，括号内写上理由已知：∠1=∠2，∠A=∠F．求证：∠C=∠D．