题目内容
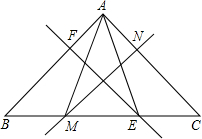 如图所示,在△ABC中,∠BAC=76°,EF,MN分别是AB,AC的垂直平分线,点E,M在BC上,则∠EAM=
如图所示,在△ABC中,∠BAC=76°,EF,MN分别是AB,AC的垂直平分线,点E,M在BC上,则∠EAM=考点:线段垂直平分线的性质
专题:
分析:根据三角形内角和定理求出∠B+∠C的度数,根据线段垂直平分线性质得出AE=BE,AM=CM,推出∠B=∠EAB,∠C=∠MAC,把求出数代入∠EAM=∠EAB+∠MAC-∠BAC,即可得出答案.
解答:解:∵∠BAC=76°,
∴∠B+∠C=180°-∠BAC=104°,
∵EF,MN分别是AB,AC的垂直平分线,
∴AE=BE,AM=CM,
∴∠B=∠EAB,∠C=∠MAC,
∴∠EAM=∠EAB+∠MAC-∠BAC=104°-76°=28°,
故答案为:28°.
∴∠B+∠C=180°-∠BAC=104°,
∵EF,MN分别是AB,AC的垂直平分线,
∴AE=BE,AM=CM,
∴∠B=∠EAB,∠C=∠MAC,
∴∠EAM=∠EAB+∠MAC-∠BAC=104°-76°=28°,
故答案为:28°.
点评:本题考查了三角形内角和定理,线段垂直平分线性质,等腰三角形的性质的应用,能综合运用性质进行推理是解此题的关键,注意:线段垂直平分线上的点到线段两个端点的距离相等.

练习册系列答案
相关题目
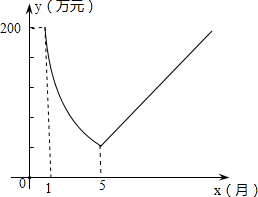 保护生态环境,建设绿色社会已经从理念变为人们的行动.某化工厂2014年1月的利润为200万元.设2014年1月为第1个月,第x个月的利润为y万元.由于排污超标,该厂决定从2014年1月底起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例.到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元(如图).
保护生态环境,建设绿色社会已经从理念变为人们的行动.某化工厂2014年1月的利润为200万元.设2014年1月为第1个月,第x个月的利润为y万元.由于排污超标,该厂决定从2014年1月底起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例.到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元(如图).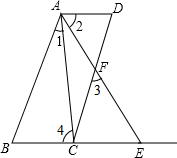 如图,已知AD∥BE,AB∥CD,∠1=∠2.求证:∠3=∠4.
如图,已知AD∥BE,AB∥CD,∠1=∠2.求证:∠3=∠4.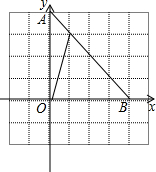 如图,等腰直角△AOB中,∠AOB=90°,点D在AB上,将△AOD绕顶点O沿顺时针方向旋转90°后得到△BOE.
如图,等腰直角△AOB中,∠AOB=90°,点D在AB上,将△AOD绕顶点O沿顺时针方向旋转90°后得到△BOE. 如图,有一条等宽的纸带,按如图所示进行折叠,求纸带重叠部分中的∠α的度数.
如图,有一条等宽的纸带,按如图所示进行折叠,求纸带重叠部分中的∠α的度数.
 如图,点C在线段AB上,点M,N分别是AC,BC的中点,且AB=14cm.
如图,点C在线段AB上,点M,N分别是AC,BC的中点,且AB=14cm.