题目内容
 如图,点E、F分别为正方形ABCD中AB、BC边的中点,连接AF、DE相交于点G,连接CG,则cos∠CGD=( )
如图,点E、F分别为正方形ABCD中AB、BC边的中点,连接AF、DE相交于点G,连接CG,则cos∠CGD=( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:正方形的性质,勾股定理,锐角三角函数的定义
专题:
分析:根据正方形的性质可得AB=AD,∠B=∠BAD=90°,再求出AE=BF,然后利用“边角边”证明△ABF和△DAE全等,根据全等三角形对应角相等可得∠AED=∠BFA,再求出∠AGE=90°,从而得到AF⊥DE,取AD的中点H,连接CH,再判断出CH垂直平分DG,根据线段垂直平分线上的点到两端点的距离相等可得CD=CG,根据等边对等角可得∠CGD=∠CDG,再求出∠CGD=∠AED,设正方形的边长为2a,求出AE,再利用勾股定理列式求出DE,然后根据锐角的余弦等于邻边比斜边列式计算即可得解.
解答:解:如图,在正方形ABCD中,AB=AD,∠B=∠BAD=90°,
∵E、F分别为AB、BC边的中点,
∴AE=BF,
在△ABF和△DAE中,
,
∴△ABF≌△DAE(SAS),
∴∠AED=∠BFA,
∵∠BAF+∠AED=∠BAF+∠BFA=90°,
∴∠AGE=90°,
∴AF⊥DE,
取AD的中点H,连接CH,
因为H是AD的中点,CH∥AF,
设CH与DG相交于点M,则MH是三角形ADG的中位线,
所以DM=GM,
所以CH垂直平分DG,
∴CD=CG,
∴∠CGD=∠CDG,
∵AB∥CD,
∴∠CGD=∠AED,
设正方形的边长为2a,则AE=a,
由勾股定理得,DE=
=
=
a,
∴cos∠AED=
=
=
,
∴cos∠CGD=cos∠AED=
.
故选D.
∵E、F分别为AB、BC边的中点,
∴AE=BF,
在△ABF和△DAE中,
|
∴△ABF≌△DAE(SAS),
∴∠AED=∠BFA,
∵∠BAF+∠AED=∠BAF+∠BFA=90°,

∴∠AGE=90°,
∴AF⊥DE,
取AD的中点H,连接CH,
因为H是AD的中点,CH∥AF,
设CH与DG相交于点M,则MH是三角形ADG的中位线,
所以DM=GM,
所以CH垂直平分DG,
∴CD=CG,
∴∠CGD=∠CDG,
∵AB∥CD,
∴∠CGD=∠AED,
设正方形的边长为2a,则AE=a,
由勾股定理得,DE=
| AE2+AD2 |
| a2+(2a)2 |
| 5 |
∴cos∠AED=
| AE |
| DE |
| a | ||
|
| ||
| 5 |
∴cos∠CGD=cos∠AED=
| ||
| 5 |
故选D.
点评:本题考查了正方形的性质,勾股定理,锐角三角函数的定义,线段垂直平分线上的点到两端点的距离相等的性质,熟记性质并作辅助线把∠CGD转化为∠AED是解题的关键.

练习册系列答案
相关题目
 小明仰视如图的两个物体,他看到的俯视图是( )
小明仰视如图的两个物体,他看到的俯视图是( )A、 |
B、 |
C、 |
D、 |
临浦是座千年老镇,昔为浙江四大米市之一,镇南临浦阳江,西依峙山,著名的陈迹有临江书舍、西施庙、日思庵、范蠡庙等.峙山海拔59米,峙山塔高高耸立在峙山顶,为千年古镇第一塔.峙山塔建于2004年,钢筋混泥土框架结构仿古楼阁式塔,八面九层,高50米,总面积千余平方米.同学们想知道3号楼到峙山的水平距离约多少米,制定以下方案:如图,同学们的眼睛、路灯顶端、塔顶在同一直线上,测量得路灯高EF=3.3米,同学们到路灯的水平距离BF=16.2米,身高是1.6米,台阶高33cm.则下列数据最接近实际距离( )


| A、1200米 |
| B、1230米 |
| C、1270米 |
| D、1310米 |
若分式
的值为0,则x的值是( )
| x2-9 |
| (x+3)2 |
| A、x=0 | B、x=-3 |
| C、x=±3 | D、x=3 |
下列四个选项中,正确的是( )
A、
| ||||
| B、2-3=-6 | ||||
C、(2-
| ||||
| D、(-5)4÷(-5)2=-52 |
根据全国第六次人口普查统计,杭州市萧山区常住人口约为20330000人,近似值20330000用科学记数法可表示为( )
| A、2.033×104人 |
| B、2.033×105人 |
| C、20.33×106人 |
| D、2.033×107人 |
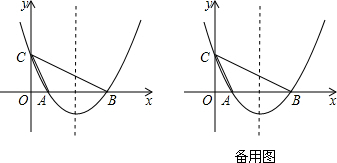
 如图,二次函数图象过点M(2,0),直线AB与该二次函数的图象交于A(0,2)、B(6,8)两点.
如图,二次函数图象过点M(2,0),直线AB与该二次函数的图象交于A(0,2)、B(6,8)两点.