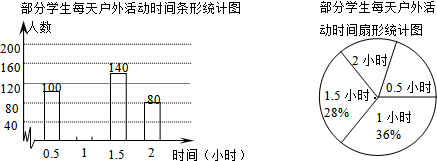
题目内容
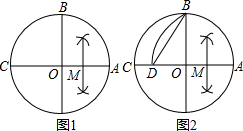 小敏在作⊙O的内接正五边形时,先做了如下几个步骤:
小敏在作⊙O的内接正五边形时,先做了如下几个步骤:(Ⅰ)作⊙O的两条互相垂直的直径,再做OA的垂直平分线交OA于点M,如图1;
(Ⅱ)以M为圆心,BM长为半径作圆弧,交CA于点D,连接BD,就得到⊙O的内接正五边形的边长a,如图2,若⊙O的半径为1,则a2的计算结果是
考点:正多边形和圆,作图—复杂作图
专题:
分析:首先连接BM,根据题意得:OB=OA=1,AD⊥OB,BM=DM,然后由勾股定理可求得BM与OD的长,继而求得BD2的值.
解答:解:如图2,连接BM,
根据题意得:OB=OA=1,AD⊥OB,BM=DM,
∵OA的垂直平分线交OA于点M,
∴OM=AM=
OA=
,
∴BM=
=
,
∴DM=
,
∴OD=DM-OM=
-
=
,
∴BD2=a2=OD2+OB2=
.
故答案为:
.
根据题意得:OB=OA=1,AD⊥OB,BM=DM,
∵OA的垂直平分线交OA于点M,
∴OM=AM=
| 1 |
| 2 |
| 1 |
| 2 |
∴BM=
| OM2+OB2 |
| ||
| 2 |
∴DM=
| ||
| 2 |
∴OD=DM-OM=
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴BD2=a2=OD2+OB2=
5-
| ||
| 2 |
故答案为:
5-
| ||
| 2 |
点评:此题考查了勾股定理、线段垂直平分线的性质以及分母有理化的知识.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
相关题目
 如图,已知菱形OABC,点C在x轴上,直线y=x经过点A,菱形OABC的边长是
如图,已知菱形OABC,点C在x轴上,直线y=x经过点A,菱形OABC的边长是 如图,△ABC内接于⊙O,D是
如图,△ABC内接于⊙O,D是
 如图,在△ABC中,DE∥BC,AD=2,AB=6,AE=3,则AC的长为
如图,在△ABC中,DE∥BC,AD=2,AB=6,AE=3,则AC的长为