题目内容
 如图,已知菱形OABC,点C在x轴上,直线y=x经过点A,菱形OABC的边长是
如图,已知菱形OABC,点C在x轴上,直线y=x经过点A,菱形OABC的边长是| 2 |
| k |
| x |
考点:菱形的性质,反比例函数图象上点的坐标特征
专题:
分析:如图,过点B作BE⊥x轴于点E,延长BA交y轴于点F.欲求k的值,只需求得四边形OEBF的面积.
解答: 解:∵直线y=x经过点A,
解:∵直线y=x经过点A,
∴∠AOC=∠FAO=45°.
如图,过点B作BE⊥x轴于点E,延长BA交y轴于点F.
∵四边形OCBA是菱形,
∴OC=BC=BA=OA=
,且AB∥OC,BC∥OA,
∴BF⊥y轴,∠AOC=∠BCE=45°,∠FAO=∠AOC=45°,
∴四边形OEBF是矩形.
∴BF=OE.
∴BE=
BC=1,AF=
OA=1,
∴OE=OC+CE=1+
∴|k|=S矩形OEBF=OE•BF=1×(1+
).
由图示知,k>0,
∴k=1+
故答案为:1+
.
 解:∵直线y=x经过点A,
解:∵直线y=x经过点A,∴∠AOC=∠FAO=45°.
如图,过点B作BE⊥x轴于点E,延长BA交y轴于点F.
∵四边形OCBA是菱形,
∴OC=BC=BA=OA=
| 2 |
∴BF⊥y轴,∠AOC=∠BCE=45°,∠FAO=∠AOC=45°,
∴四边形OEBF是矩形.
∴BF=OE.
∴BE=
| ||
| 2 |
| ||
| 2 |
∴OE=OC+CE=1+
| 2 |
∴|k|=S矩形OEBF=OE•BF=1×(1+
| 2 |
由图示知,k>0,
∴k=1+
| 2 |
故答案为:1+
| 2 |
点评:本题考查了菱形的性质,反比例函数图象上点的坐标特征.根据菱形的性质求得BE、OE的长度是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F. 如图,已知∠MON=45°,OA1=1,作正方形A1B1C1A2,面积记作S1;再作第二个正方形A2B2C2A3,面积记作S2;继续作第三个正方形A3B3C3A4,面积记作S3;点A1、A2、A3、A4…在射线ON上,点B1、B2、B3、B4…在射线OM上,…依此类推,则第4个正方形的面积S4=
如图,已知∠MON=45°,OA1=1,作正方形A1B1C1A2,面积记作S1;再作第二个正方形A2B2C2A3,面积记作S2;继续作第三个正方形A3B3C3A4,面积记作S3;点A1、A2、A3、A4…在射线ON上,点B1、B2、B3、B4…在射线OM上,…依此类推,则第4个正方形的面积S4=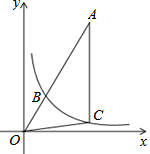 反比例函数y=
反比例函数y=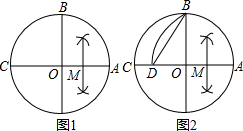 小敏在作⊙O的内接正五边形时,先做了如下几个步骤:
小敏在作⊙O的内接正五边形时,先做了如下几个步骤: