题目内容
12. 如图,菱形ABCD中,AB=8,∠ABC=60°,E是CD的中点,在对角线AC有一动点P,在某个位置存在PD+PE的和最小,则这个最小值为4$\sqrt{7}$.
如图,菱形ABCD中,AB=8,∠ABC=60°,E是CD的中点,在对角线AC有一动点P,在某个位置存在PD+PE的和最小,则这个最小值为4$\sqrt{7}$.
分析 首先连接BE,过点E作EF⊥BC于点F,由四边形ABCD是菱形,可得BE是PD+PE的和最小值,然后由菱形ABCD中,AB=8,∠ABC=60°,E是CD的中点,利用三角函数的知识即可求得CF与EF的长,再利用勾股定理求得BE的长.
解答 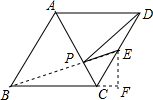 解:连接BE,过点E作EF⊥BC于点F,
解:连接BE,过点E作EF⊥BC于点F,
∵四边形ABCD是菱形,
∴点B,D关于AC对称,
∴BE是PD+PE的和最小值,
∵菱形ABCD中,AB=8,∠ABC=60°,
∴BC=CD=AB=8,AB∥CD,
∴∠ECF=∠ABC=60°,
∵E是CD的中点,
∴CE=$\frac{1}{2}$CD=4,
∴CF=CE•cos60°=4×$\frac{1}{2}$=2,EF=CF•sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴BF=BC+CF=10,
∴BE=$\sqrt{B{F}^{2}+E{F}^{2}}$=4$\sqrt{7}$.
即这个最小值为4$\sqrt{7}$.
故答案为:4$\sqrt{7}$.
点评 此题考查了最短路径问题、菱形的性质、勾股定理以及三角函数等知识.注意准确找到点P的位置是解此题的关键.

练习册系列答案
相关题目
3.两个多边形相似的条件是( )
| A. | 对应角相等 | B. | 对应角相等且对应边成比例 | ||
| C. | 对应角相等或对应边成比例 | D. | 对应边成比例 |
7.下列等式成立的是( )
| A. | 2$\sqrt{2}$-$\sqrt{2}$=2 | B. | $\sqrt{(2014)^{2}}$=2014 | C. | $\sqrt{(1-\sqrt{2})^{2}}$=1-$\sqrt{2}$ | D. | $\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{{3}^{2}}$-$\sqrt{{2}^{2}}$ |
17. 已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:
已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:
(1)求该二次函数的表达式;
(2)当x=6时,求y的值;
(3)在所给坐标系中画出该二次函数的图象.
 已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:
已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 5 | 2 | 1 | 2 | 5 | … |
(2)当x=6时,求y的值;
(3)在所给坐标系中画出该二次函数的图象.
4.点A(-1,1)是反比例函数y=$\frac{m}{x}$的图象上一点,则m的值为( )
| A. | 0 | B. | -2 | C. | -1 | D. | 1 |
 如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.
如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形. 一快车和一慢车沿相同的路线从A地到B地,所行路程与时间的图象如图,则下列结论正确的个数是( )
一快车和一慢车沿相同的路线从A地到B地,所行路程与时间的图象如图,则下列结论正确的个数是( )