题目内容
15.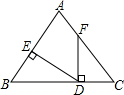 如图,点D在边BC上,DE⊥AB,DF⊥BC,垂足分别为点E、D,BD=CF,BE=CD.若∠AFD=140°,则∠EDF=50°.
如图,点D在边BC上,DE⊥AB,DF⊥BC,垂足分别为点E、D,BD=CF,BE=CD.若∠AFD=140°,则∠EDF=50°.
分析 由∠AFD=140°知∠DFC=40°,根据“AAS”证△BDE≌△CFD得∠BDE=∠CFD=40°,从而由∠EDF=180°-∠FDC-∠BDE可得答案.
解答 解:∵∠AFD=140°,
∴∠DFC=40°,
∵DE⊥AB,DF⊥BC,
∴∠DEB=∠FDC=90°,
在△BDE和△CFD中,
∵$\left\{\begin{array}{l}{BD=CF}\\{BE=CD}\\{∠DEB=∠FDC}\end{array}\right.$,
∴△BDE≌△CFD(AAS),
∴∠BDE=∠CFD=40°,
∴∠EDF=180°-∠FDC-∠BDE=50°,
故答案为:50°.
点评 本题主要考查全等三角形的判定与性质及直角三角形的性质,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
1.已知反比例函数y=$\frac{2}{x}$,则在这个反比例函数图象上的点是( )
| A. | (-2,1) | B. | (1,2) | C. | (1,-2) | D. | (-2,-2) |
5.已知:x-2y=-3,则代数式(2y-x)2-2x+4y-1的值为( )
| A. | 2 | B. | 14 | C. | -4 | D. | 0 |
 如图,在△ABC中,BP、AP是∠ABC、∠BAC的角平分线,交点为P,PD⊥BC于D,PE⊥AC于E,PD=4.则PE=4.
如图,在△ABC中,BP、AP是∠ABC、∠BAC的角平分线,交点为P,PD⊥BC于D,PE⊥AC于E,PD=4.则PE=4.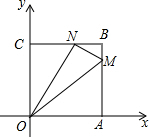 如图,在平面直角坐标系中,四边形OABC是边长为4的正方形,M(4,m)、N(n,4)分别是AB、BC上的两个动点,且ON⊥MN,当OM最小时,m+n=5.
如图,在平面直角坐标系中,四边形OABC是边长为4的正方形,M(4,m)、N(n,4)分别是AB、BC上的两个动点,且ON⊥MN,当OM最小时,m+n=5.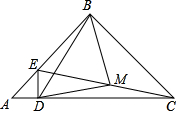 已知在△ABC中,∠ABC=90°,AB=BC=8cm,点D为AC一点,过点D作DE⊥AC交线段AB于点E,点M为EC的中点.
已知在△ABC中,∠ABC=90°,AB=BC=8cm,点D为AC一点,过点D作DE⊥AC交线段AB于点E,点M为EC的中点.