题目内容
2.抛物线y=ax2+bx+c的对称轴为直线x=2,与x轴的一个交点坐标为(-1,0),则一元二次方程ax2+bx+c=0的解为x1=-1,x2=5;若a>0,则一元二次不等式ax2+bx+c>0的解为x<-1或x>5.分析 首先求得:(-1,0)关于x=2的对称点,即求出二次函数与x轴的交点,然后根据二次函数的图象的性质判断.
解答 解:(-1,0)关于x=2的对称点是(5,0).
则一元二次方程ax2+bx+c=0的解为x1=-1,x2=5;
当a>0时,二次函数的开口向上,则一元二次不等式ax2+bx+c>0的解是x<-1或x>5.
故答案是:x1=-1,x2=5;x<-1或x>5.
点评 本题考查了二次函数与不等式的关系,以及二次函数的图象与x轴的交点坐标,求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.

练习册系列答案
相关题目
10.若不等式组$\left\{\begin{array}{l}{x<2a-1}\\{x>3}\end{array}\right.$无解,则a的取值范围是( )
| A. | a≤2 | B. | a>2 | C. | a>3 | D. | a≥3 |
 某校数学兴趣小组在探究如何求tan 15°,cos15°的值,经过自主思考、合作交流讨论,得到以下思路:
某校数学兴趣小组在探究如何求tan 15°,cos15°的值,经过自主思考、合作交流讨论,得到以下思路: 如图,正方形AOCB在平面直角坐标系x0y中,点O为原点,点B在反比例函数y=$\frac{16}{x}$(x>0)图象上.
如图,正方形AOCB在平面直角坐标系x0y中,点O为原点,点B在反比例函数y=$\frac{16}{x}$(x>0)图象上. 在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(-2,6),C(2,2)两点.
在平面直角坐标系xOy中,抛物线y=ax2+bx+2过B(-2,6),C(2,2)两点.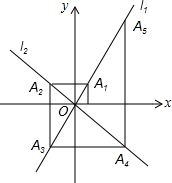 如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2017的坐标为(21008,21009).
如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2017的坐标为(21008,21009). 正方形ABCD中,对角线AC,BD相交于点O,DE平分∠ADO交AC于点E,把△ADE沿AD翻折,得到△ADE′,点F是DE的中点,连接AF,BF,E′F.若AE=$\sqrt{2}$.则四边形ABFE′的面积是$\frac{6+3\sqrt{2}}{2}$.
正方形ABCD中,对角线AC,BD相交于点O,DE平分∠ADO交AC于点E,把△ADE沿AD翻折,得到△ADE′,点F是DE的中点,连接AF,BF,E′F.若AE=$\sqrt{2}$.则四边形ABFE′的面积是$\frac{6+3\sqrt{2}}{2}$. 如图,在平面直角坐标系xOy中,以点O为圆心的圆分别交x轴的正半轴于点M,交y轴的正半轴于点N.劣弧$\widehat{MN}$的长为$\frac{6}{5}$π,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A、B.
如图,在平面直角坐标系xOy中,以点O为圆心的圆分别交x轴的正半轴于点M,交y轴的正半轴于点N.劣弧$\widehat{MN}$的长为$\frac{6}{5}$π,直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点A、B.