Question

7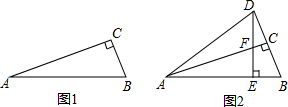．如图1，在△ABC中，∠C=90°，AB=1，∠A=α，则cosα=$\frac{AC}{AB}=AC$，现将△ABC沿AC折叠，得到△ADC，如图2，易知B、C、D三点共线，∠DAB=2α（其中0°＜α＜45°）．
过点D作DE⊥AB于点E．
∵∠DCA=∠DEA=90°，∠DFC=∠AFE，
∴∠BDE=∠BAC=α，
∵BD=2BC=2sinα，
∴BE=BD•sinα=2•sinα•sinα=2sin²α，
∴AE=AB-BE=1-2sin²α，
∴cos2α=cos∠DAE=$\frac{AE}{AD}=\frac{1-2si{n}^{2}α}{1}=1-2si{n}^{2}α$．
阅读以上内容，回答下列问题：
（1）如图1，若BC=$\frac{1}{3}$，则cosα=$\frac{2\sqrt{2}}{3}$，cos2α=$\frac{7}{9}$；
（2）求出sin2α的表达式（用含sinα或cosα的式子表示）．

Answer 1

分析 （1）先根据勾股定理计算出AC=$\frac{2\sqrt{2}}{3}$，则根据正弦和余弦的定义得到cosα=$\frac{2\sqrt{2}}{3}$，sinα=BC=$\frac{1}{3}$，然后根据题中的结论cos2α=1-2sin²α进行计算；
（2）根据三角函数的定义，在Rt△BDE中得到cos∠BDE=$\frac{DE}{BD}$，则DE=2sinα•cosα，然后在Rt△ADE中得到sin∠DAE=$\frac{DE}{AD}$，即有sin2α=2sinα•cosα．

解答 解：（1）在Rt△ABC中，∵AB=1，BC=$\frac{1}{3}$，
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\frac{2\sqrt{2}}{3}$，
∴cosα=$\frac{2\sqrt{2}}{3}$，
sinα=BC=$\frac{1}{3}$，
∴cos2α=1-2×（$\frac{1}{3}$）²=$\frac{7}{9}$；
故答案为：$\frac{2\sqrt{2}}{3}$，$\frac{7}{9}$；

（2）根据题意得BD=2sinα，∠BDE=α，
在Rt△BDE中，∵cos∠BDE=$\frac{DE}{BD}$，
∴DE=BD•cosα=2sinα•cosα，
在Rt△ADE中，∵sin∠DAE=$\frac{DE}{AD}$，
∴sin2α=$\frac{2sinα•cosα}{1}$=2sinα•cosα．

点评 本题考查了解直角三角形：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．也考查了阅读理解能力．