题目内容
20. 如图,点A、B在⊙O上,且AO=2,∠AOB=120°,则阴影部分面积为$\frac{4π}{3}$-$\sqrt{3}$.
如图,点A、B在⊙O上,且AO=2,∠AOB=120°,则阴影部分面积为$\frac{4π}{3}$-$\sqrt{3}$.
分析 过O作OC⊥AB于C,根据垂径定理得到AC=BC;而∠AOB=120°,OA=OB,根据等腰三角形的性质得∠A=30°;在Rt△OAC中,OA=2,∠A=30°,根据含30度的直角三角形三边的关系得到OC和AC,则可求出AB,最后根据扇形的面积公式和三角形的面积公式利用S阴影部分=S扇形OAB-S△OAB进行计算即可.
解答  解:过O作OC⊥AB于C,如图,
解:过O作OC⊥AB于C,如图,
∴AC=BC,
而∠AOB=120°,OA=OB,
∴∠A=$\frac{1}{2}$(180°-120°)=30°,
在Rt△OAC中,OA=2,∠A=30°,
∴OC=1,AC=$\sqrt{3}$,
∴AB=2$\sqrt{3}$,
∴S阴影部分=S扇形OAB-S△OAB
=$\frac{120•π•{2}^{2}}{360}$-$\frac{1}{2}$•1•2$\sqrt{3}$
=$\frac{4π}{3}$-$\sqrt{3}$.
故答案为$\frac{4π}{3}$-$\sqrt{3}$.
点评 本题考查了扇形的面积公式:S=$\frac{nπ{R}^{2}}{360}$;也考查了垂径定理和等腰三角形的性质以及含30度的直角三角形三边的关系.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
8. 已知抛物线y=$\frac{1}{2}$(x-3)2-2的部分图象(如图),图象再次与x轴相交时的坐标是( )
已知抛物线y=$\frac{1}{2}$(x-3)2-2的部分图象(如图),图象再次与x轴相交时的坐标是( )
 已知抛物线y=$\frac{1}{2}$(x-3)2-2的部分图象(如图),图象再次与x轴相交时的坐标是( )
已知抛物线y=$\frac{1}{2}$(x-3)2-2的部分图象(如图),图象再次与x轴相交时的坐标是( )| A. | (2,0) | B. | (3,0) | C. | (4,0) | D. | (5,0) |
 把厚度相同的字典整齐地叠放在桌面上,已知字典的离地高度与字典本数成一次函数,根据图中所示的信息,给出下列结论:
把厚度相同的字典整齐地叠放在桌面上,已知字典的离地高度与字典本数成一次函数,根据图中所示的信息,给出下列结论: 如图,二次函数y=ax2+bx+c的图象经过点(-1,2),且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1.下列结论:①4a-2b+c<0;②2a-b<0;③b<1;④a>-$\frac{1}{2}$;⑤(a+c)2<b2中正确的有①②⑤(将你认为正确的结论番号都填出来)
如图,二次函数y=ax2+bx+c的图象经过点(-1,2),且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1.下列结论:①4a-2b+c<0;②2a-b<0;③b<1;④a>-$\frac{1}{2}$;⑤(a+c)2<b2中正确的有①②⑤(将你认为正确的结论番号都填出来) 如图,在Rt△ABC中∠ACB=90°,斜边上的中线CF=8cm,DE是△ABC的中位线,则下列叙述中,正确的序号为( )
如图,在Rt△ABC中∠ACB=90°,斜边上的中线CF=8cm,DE是△ABC的中位线,则下列叙述中,正确的序号为( )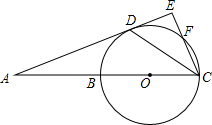 如图,直线AD切⊙O于点D,直线AB经过圆心O,交⊙O于点B、C,CE⊥AD,垂足为E,CE交⊙O于点F,连接CD.
如图,直线AD切⊙O于点D,直线AB经过圆心O,交⊙O于点B、C,CE⊥AD,垂足为E,CE交⊙O于点F,连接CD. △ABC中,E,F分别是AC,AB的中点,连接EF,则S△AEF:S△ABC=$\frac{1}{4}$.
△ABC中,E,F分别是AC,AB的中点,连接EF,则S△AEF:S△ABC=$\frac{1}{4}$. 如图,△ABC的外角平分线CP和内角平分线BP相交于点P,若∠BPC=80°,则∠CAP=10.
如图,△ABC的外角平分线CP和内角平分线BP相交于点P,若∠BPC=80°,则∠CAP=10.