题目内容
5.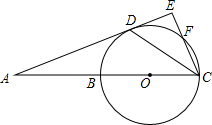 如图,直线AD切⊙O于点D,直线AB经过圆心O,交⊙O于点B、C,CE⊥AD,垂足为E,CE交⊙O于点F,连接CD.
如图,直线AD切⊙O于点D,直线AB经过圆心O,交⊙O于点B、C,CE⊥AD,垂足为E,CE交⊙O于点F,连接CD.(1)猜想$\widehat{BD}$和$\widehat{FD}$的数量关系,并证明;
(2)若sin∠DCE=$\frac{3}{5}$,CE=8,求⊙O的半径.
分析 (1)$\widehat{BD}$=$\widehat{FD}$,连接OD,由切线的性质和已知条件证明圆周角∠OCD=∠DCE即可;
(2)连接BD,易求CD的长,再由相等的角则其三角函数值也相等可求出sin∠DCB的值,进而可得到直径BC的长,圆的半径也就求出.
解答 解:(1)$\widehat{BD}$=$\widehat{FD}$,理由如下:
连接OD,
∵直线AD切⊙O于点D,
∴OD⊥AE,
∵CE⊥AD,垂足为E,
∴OD∥CE,
∴∠ODC=∠DCE,
∵OD=OC,
∴∠ODC=∠OCD,
∴∠OCD=∠DCE,
∴$\widehat{BD}$=$\widehat{FD}$; (2)连接BD,
(2)连接BD,
∵sin∠DCE=$\frac{3}{5}$,
∴$\frac{DE}{CD}=\frac{3}{5}$,
∵CE=8,∠E=90°,
∴CD=10,
∵∠OCD=∠DCE,
∴sin∠DCB=$\frac{3}{5}$,
∴$\frac{DC}{BC}=\frac{4}{5}$,
∴BC=$\frac{25}{2}$,
∴⊙O的半径=$\frac{25}{4}$.
点评 本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
13.不等式x+1>3的解集是( )
| A. | x>1 | B. | x>-2 | C. | x>2 | D. | x<2 |
14. (1)计算:$\sqrt{4}$tan45°$+(\frac{1}{3})^{-1}-2cos60°+(π-2011)^{0}$
(1)计算:$\sqrt{4}$tan45°$+(\frac{1}{3})^{-1}-2cos60°+(π-2011)^{0}$
(2)解方程:x2-4x=3
(3)如果代数式m2-8m-12与5m-42的值相等,求-2m+5的值.
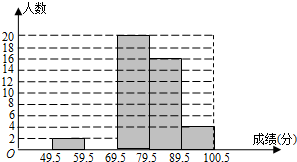
(4)某校数学兴趣小组成员小华对本班上期期末考试数学成绩作了统计分析,绘制成如下频数、频率分布表和频数分布直方图.请你根据图表提供的信息,解答下列问题:
①频数、频率分布表中a=8,b=0.08;
②补全频数分布直方图;
③数学老师准备从不低于90分的学生中选1人介绍学习经验,那么取得了93分的小华
被选上的概率是多少?
 (1)计算:$\sqrt{4}$tan45°$+(\frac{1}{3})^{-1}-2cos60°+(π-2011)^{0}$
(1)计算:$\sqrt{4}$tan45°$+(\frac{1}{3})^{-1}-2cos60°+(π-2011)^{0}$(2)解方程:x2-4x=3
(3)如果代数式m2-8m-12与5m-42的值相等,求-2m+5的值.
(4)某校数学兴趣小组成员小华对本班上期期末考试数学成绩作了统计分析,绘制成如下频数、频率分布表和频数分布直方图.请你根据图表提供的信息,解答下列问题:
①频数、频率分布表中a=8,b=0.08;
②补全频数分布直方图;
③数学老师准备从不低于90分的学生中选1人介绍学习经验,那么取得了93分的小华
被选上的概率是多少?
| 分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合计 |
| 频数 | 2 | a | 20 | 16 | 4 | 50 |
| 频率 | 0.04 | 0.16 | 0.40 | 0.32 | b | 1 |
12.如图,下列四个几何体中,从正面看、从上面看、从左面看,其视图中只有两个相同的是( )
| A. |  正方体 | B. |  球体 | C. |  正三棱柱 | D. |  圆柱 |
 如图所示.
如图所示. 如图,点A、B在⊙O上,且AO=2,∠AOB=120°,则阴影部分面积为$\frac{4π}{3}$-$\sqrt{3}$.
如图,点A、B在⊙O上,且AO=2,∠AOB=120°,则阴影部分面积为$\frac{4π}{3}$-$\sqrt{3}$. 如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0;②2a+b=0;③a+b+c>0;④△>0;⑤4a-2b+c<0,其中正确的个数为( )
如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0;②2a+b=0;③a+b+c>0;④△>0;⑤4a-2b+c<0,其中正确的个数为( )