题目内容
2．
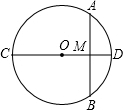如图，CD是⊙O的直径，CD⊥AB于M，已知AB=8，MO=3，则⊙O的半径为5．
分析 连接OB，根据垂径定理求出BM，根据勾股定理得出方程，求出方程的解即可．
解答 证明：连接OB，设半径为rcm，
∵CD是⊙O的直径，CD⊥AB，
∴BM=$\frac{1}{2}AB=4$，
在Rt△OBM中，∵OB2=OM2+MB2，
∴r2=32+42，
r=5，
答：⊙O的半径为5，
故答案为：5
点评 本题考查了垂径定理和勾股定理的应用，关键是能构造直角三角形并得出方程．
练习册系列答案
相关题目
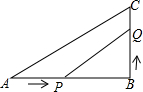如图，在△ABC中，∠B=90°，AB=6cm，点P从点A开始沿AB向B以1cm/s的速度移动，点Q从点B开始沿BC向C点以2cm/s的速度移动，如果P，Q分别从A，B同时出发，2或4秒后△PBQ的面积等于8cm2．
如图，已知正方形ABCD，∠DBC的平分线交DC于点E，作EF⊥BD于点F，作FG⊥BC于点G，则$\frac{FG}{GC}$=$\sqrt{2}$+1．
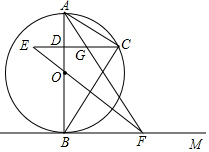如图，AB是⊙O的直径，直线BM经过点B，点C在右半圆上移动（与点A、B不重合），过点C作CD⊥AB，垂足为D，连接CA、CB，∠CBM=∠BAC，点F在射线BM上移动（点M在点B的右边），在移动过程中始终保持OF∥AC．