题目内容
20. 为了改善小区环境,某小区决定要在一块一边靠墙(墙的最大可用长度为10米)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40米的栅栏围住(如图).若设绿化带的BC边长为x米,绿化带的面积为y平方米.
为了改善小区环境,某小区决定要在一块一边靠墙(墙的最大可用长度为10米)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40米的栅栏围住(如图).若设绿化带的BC边长为x米,绿化带的面积为y平方米.(1)求y与x之间的函数关系式及自变量的x的取值范围.
(2)栅栏BC为多少米时,花圃的面积最大?最大面积为多少?
分析 (1)依题意易求得y与x的函数关系式以及x的取值范围;
(2)把(1)的函数关系式用配方法化简,进而结合二次函数增减性求得y的最大值即可.
解答 解:(1)由题意得:y=x×$\frac{40-x}{2}$=-$\frac{1}{2}$x2+20x,
自变量x的取值范围是:0<x≤10;
(2)y=-$\frac{1}{2}$x2+20x
=-$\frac{1}{2}$(x-20)2+200
∵20>10,
∴当x=10时,y有最大值150平方米,
即栅栏BC为10米时,花圃的面积最大,最大面积为150平方米.
点评 本题考查的是二次函数的实际应用.正确利用二次函数增减性求出最值是解题关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
5. 如图,平行四边形ABOC中,对角线AO与BC相交于点E,双曲线y=$\frac{k}{x}$(k<0)经过C,E两点,若平行四边形ABOC的面积为36,则k的值是( )
如图,平行四边形ABOC中,对角线AO与BC相交于点E,双曲线y=$\frac{k}{x}$(k<0)经过C,E两点,若平行四边形ABOC的面积为36,则k的值是( )
 如图,平行四边形ABOC中,对角线AO与BC相交于点E,双曲线y=$\frac{k}{x}$(k<0)经过C,E两点,若平行四边形ABOC的面积为36,则k的值是( )
如图,平行四边形ABOC中,对角线AO与BC相交于点E,双曲线y=$\frac{k}{x}$(k<0)经过C,E两点,若平行四边形ABOC的面积为36,则k的值是( )| A. | -$\frac{5}{2}$ | B. | -$\frac{10}{3}$ | C. | -4 | D. | -5 |
10.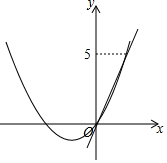 如图,抛物线y=$\frac{1}{2}$x2+$\frac{3}{2}$x与直线y=kx的交点A的纵坐标是5,则不等式$\frac{1}{2}$x2+$\frac{3}{2}$x-kx>0的解集是( )
如图,抛物线y=$\frac{1}{2}$x2+$\frac{3}{2}$x与直线y=kx的交点A的纵坐标是5,则不等式$\frac{1}{2}$x2+$\frac{3}{2}$x-kx>0的解集是( )
 如图,抛物线y=$\frac{1}{2}$x2+$\frac{3}{2}$x与直线y=kx的交点A的纵坐标是5,则不等式$\frac{1}{2}$x2+$\frac{3}{2}$x-kx>0的解集是( )
如图,抛物线y=$\frac{1}{2}$x2+$\frac{3}{2}$x与直线y=kx的交点A的纵坐标是5,则不等式$\frac{1}{2}$x2+$\frac{3}{2}$x-kx>0的解集是( )| A. | x>0 | B. | -2<x<0 | C. | -5<x<2 | D. | x<0或x>2 |
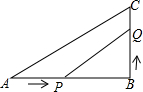 如图,在△ABC中,∠B=90°,AB=6cm,点P从点A开始沿AB向B以1cm/s的速度移动,点Q从点B开始沿BC向C点以2cm/s的速度移动,如果P,Q分别从A,B同时出发,2或4秒后△PBQ的面积等于8cm2.
如图,在△ABC中,∠B=90°,AB=6cm,点P从点A开始沿AB向B以1cm/s的速度移动,点Q从点B开始沿BC向C点以2cm/s的速度移动,如果P,Q分别从A,B同时出发,2或4秒后△PBQ的面积等于8cm2.
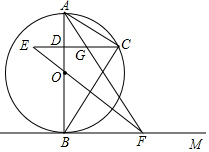 如图,AB是⊙O的直径,直线BM经过点B,点C在右半圆上移动(与点A、B不重合),过点C作CD⊥AB,垂足为D,连接CA、CB,∠CBM=∠BAC,点F在射线BM上移动(点M在点B的右边),在移动过程中始终保持OF∥AC.
如图,AB是⊙O的直径,直线BM经过点B,点C在右半圆上移动(与点A、B不重合),过点C作CD⊥AB,垂足为D,连接CA、CB,∠CBM=∠BAC,点F在射线BM上移动(点M在点B的右边),在移动过程中始终保持OF∥AC.