题目内容
10．二次函数：y=x2-2mx-3+2m随着字母m取值不同，其函数在坐标平面内移动，则此函数图象一定不经过（m，0）点．分析 首先把二次函数的解析式化为顶点式，由顶点坐标即可得到结论．
解答 解：二次函数y=x2-2mx-3+2m可化为y=（x-m）2-（m2-2m+3），
∴顶点坐标为（m，m2-2m+3），
∵m2-2m+3=0时，△=（-2）2-4×3＜0，
∴m2-2m+3≠0，
∴此函数图象一定不经过（m，0）点，
故答案为：（m，0）．
点评 本题考查了二次函数的性质，求二次函数的顶点坐标，熟记二次函数的性质是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
两个有理数a、b在数轴上的位置如图所示，且|a|＜|b|，试比较a、b、-a、-b、0的大小关系．
如图，△ABC的高AD，BE相交于点F．
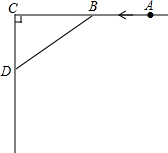如图，AC⊥CD，甲、乙两人分别骑自行车从相距10km的A，C两地同时出发，各沿箭头所指方向前进．已知甲的速度是16km/h，乙的速度是12km/h，且当甲到达C地时两人停止运动．问：出发多少时间后两人相距最近？最近距离为多少千米？
5．
已知有理数a、b在数轴上表示的点如图所示，则下列式子中正确的是（ ）
已知有理数a、b在数轴上表示的点如图所示，则下列式子中正确的是（ ）| A． | a+b＞0 | B． | a-b＜0 | C． | ab＞0 | D． | $\frac{a}{b}＜0$ |
19．下列各式与$\sqrt{3}$不是同类二次根式的是（ ）
| A． | $\sqrt{12}$ | B． | $\sqrt{27}$ | C． | $\sqrt{8}$ | D． | $\sqrt{75}$ |