题目内容
9. 如图,菱形ABCD中,AE平分∠BAC交BC于E,AF平分∠CAD交CD于F,求证:AE=AF.
如图,菱形ABCD中,AE平分∠BAC交BC于E,AF平分∠CAD交CD于F,求证:AE=AF.
分析 欲证明AE=AF,只要证明△ACE≌△ACF即可.
解答 证明:∵四边形 ABCD是菱形,
ABCD是菱形,
∴∠BAC=∠DAC,∠ACB=∠ACD,
∵EA平分∠BAC,FA平分∠DAC,
∴∠CAE=∠CAF,
在△CAE和△CAF中,
$\left\{\begin{array}{l}{∠CAE=∠CAF}\\{∠ACE=∠ACF}\\{AC=AC}\end{array}\right.$,
∴△ACE≌△ACF,
∴AE=AF.
点评 本题考查全等三角形的判定和性质、菱形的性质.角平分线的性质等知识,解题的关键是熟练掌握全等三角形的判定和性质,属于基础题,中考常考题型.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
20.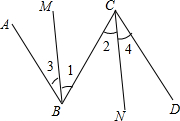 如图已知∠3=∠4,要得到AB∥CD,则需要的条件不是( )
如图已知∠3=∠4,要得到AB∥CD,则需要的条件不是( )
 如图已知∠3=∠4,要得到AB∥CD,则需要的条件不是( )
如图已知∠3=∠4,要得到AB∥CD,则需要的条件不是( )| A. | ∠1=∠2 | B. | ∠1=∠3且∠2=∠4 | ||
| C. | BM∥CN | D. | ∠1与∠2互补且不相等 |
18. 如图是某个几何体的三视图,则该几何体的形状是( )
如图是某个几何体的三视图,则该几何体的形状是( )
 如图是某个几何体的三视图,则该几何体的形状是( )
如图是某个几何体的三视图,则该几何体的形状是( )| A. | 长方体 | B. | 圆锥 | C. | 三棱锥 | D. | 直三棱柱 |
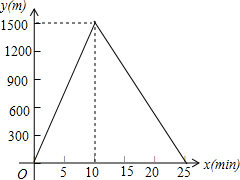 小明从家到达A地后立即返回,他离家的路程y(m)与所用时间x(min)的函数图象如图所示,小明去时路过报亭C与返回时路过报亭C相隔10min.
小明从家到达A地后立即返回,他离家的路程y(m)与所用时间x(min)的函数图象如图所示,小明去时路过报亭C与返回时路过报亭C相隔10min.
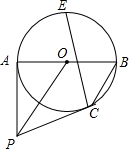 如图,AB是⊙O的直径,点P是⊙O外一点,PA切⊙O于点A,连接OP,过点B作BC∥OP交⊙O于点C,点E是$\widehat{AB}$的中点.
如图,AB是⊙O的直径,点P是⊙O外一点,PA切⊙O于点A,连接OP,过点B作BC∥OP交⊙O于点C,点E是$\widehat{AB}$的中点.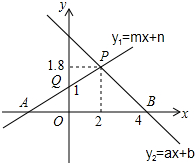 如图,根据图中信息解答下列问题:
如图,根据图中信息解答下列问题: