题目内容
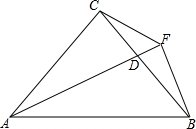 在Rt△ABC中,∠ACB=90°,AC=BC.
在Rt△ABC中,∠ACB=90°,AC=BC.(1)若∠AFC=45°,求证:BF⊥AD;
(2)若AD为角平分线,BF⊥AD,连接CE.
①求证:AD=2BF;
②求证:AB=AC+CD.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)由∠AFC=∠ABC可得出A、B、F、C四点共圆,再结合圆周角定理可得出∠AFB=∠ACB=90°,可得出结论;
(2)①延长BF交AC的延长线于点E,则由条件可知△ABE为等腰三角形,结合条件可证明△ACD≌△BCE,可得出结论,
②过D作DG⊥AB于点G,可证得△ACD≌△AGD,得到AC=AE,CD=DE,且DE=DB,可得出结论.
(2)①延长BF交AC的延长线于点E,则由条件可知△ABE为等腰三角形,结合条件可证明△ACD≌△BCE,可得出结论,
②过D作DG⊥AB于点G,可证得△ACD≌△AGD,得到AC=AE,CD=DE,且DE=DB,可得出结论.
解答:(1)证明:∵AC=BC,∠ACB=90°,
∴∠ABC=∠AFC=45°,
∴A、B、F、C四点共圆,
∴∠AFB=∠ACB=90°,
∴BF⊥AD;
(2)证明:①如图1,延长BF交AC的延长线于点E,
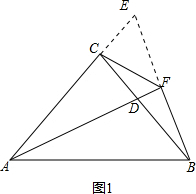
∵AD为∠CAB的平分线,AF⊥BF,
∴∠AEB=∠ABE,
∴AE=AB,
∴BE=2BF,∠ECAD=∠EBC,
在Rt△ACD和Rt△BCE中,
,
∴△ACD≌△BCE(ASA),
∴AC=BE=2BF;
②如图2,过D作DG⊥AB于点G,
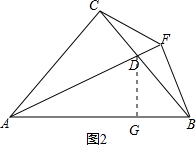
∵AD平分∠CAB,
∴DC=DG,
在Rt△ACD和Rt△AGD中,
,
∴Rt△ACD≌Rt△AGD(HL),
∴AG=AC,GD=CD,
∵∠ACB=90°,AC=BC
∴∠DBG=45°,
∴BG=DG,
∴AB=AG+GB=AC+DG=AC+CD.
∴∠ABC=∠AFC=45°,
∴A、B、F、C四点共圆,
∴∠AFB=∠ACB=90°,
∴BF⊥AD;
(2)证明:①如图1,延长BF交AC的延长线于点E,

∵AD为∠CAB的平分线,AF⊥BF,
∴∠AEB=∠ABE,
∴AE=AB,
∴BE=2BF,∠ECAD=∠EBC,
在Rt△ACD和Rt△BCE中,
|
∴△ACD≌△BCE(ASA),
∴AC=BE=2BF;
②如图2,过D作DG⊥AB于点G,

∵AD平分∠CAB,
∴DC=DG,
在Rt△ACD和Rt△AGD中,
|
∴Rt△ACD≌Rt△AGD(HL),
∴AG=AC,GD=CD,
∵∠ACB=90°,AC=BC
∴∠DBG=45°,
∴BG=DG,
∴AB=AG+GB=AC+DG=AC+CD.
点评:本题主要考查全等三角形的判定和性质及等腰三角形、角平分线的性质的应用,寻找、构造三角形全等是解题的关键.

练习册系列答案
相关题目
下列关于相反数的说法中,错误的是( )
| A、-2的相反数是2 |
| B、m和-m互为相反数 |
| C、和为零的两个数互为相反数 |
| D、零没有相反数 |

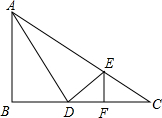 如图,在△ABC中,∠B=90°,AB=8,BC=16,D在边BC上,BD=6,AD⊥DE交AC于点E,EF⊥BC于点F.
如图,在△ABC中,∠B=90°,AB=8,BC=16,D在边BC上,BD=6,AD⊥DE交AC于点E,EF⊥BC于点F.
 根据俯视图画出主视图和左视图.
根据俯视图画出主视图和左视图.