��Ŀ����
��ͼ����ƽ��ֱ������ϵ�У�ֱ��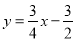 ��������
��������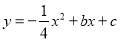 ����A��B���㣬��A��x���ϣ���B�ĺ�����Ϊ��8��
����A��B���㣬��A��x���ϣ���B�ĺ�����Ϊ��8��
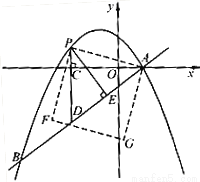
��1����������ߵĽ���ʽ��
��2����P��ֱ��AB�Ϸ�����������һ���㣨�����A��B�غϣ�������P��x��Ĵ��ߣ�����ΪC����ֱ��AB�ڵ�D����PE��AB�ڵ�E��
�����PDE���ܳ�Ϊl����P�ĺ�����Ϊx����l����x�ĺ�����ϵʽ�������l�����ֵ��
������PA����PAΪ������ͼ��ʾһ���������APFG�����ŵ�P���˶��������εĴ�С��λ��Ҳ��֮�ı䣮������F��Gǡ������y����ʱ�������Ӧ�ĵ�P�����꣮
��1����2����15 �� �������������������1������ֱ�߽���ʽ�����A��B�����꣬�����ô���ϵ��������κ�������ʽ��𣻣�2��������ֱ�߽���ʽ�������߽���ʽ��ʾ��PD��������ͬ�ǵ������������DPE=��BAO������ֱ��kֵ�����BAO�����Һ�����ֵ��Ȼ���ʾ��PE��DE���ٸ��������ε��ܳ���ʽ��ʽ�������ɵý⣬�ٸ��ݶ��κ�������ֵ�����𣻢ڷ֣�i����G��y����ʱ������P��PH��x����H��...
��ϰ��ϵ�д�
�����Ŀ
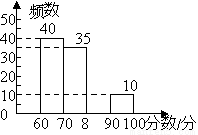
ijѧУ��1500��ѧ���μ��조�Ұ����ǵĿ��á�Ϊ�����ͼƬ�������������������ȡ���ֲ���ѧ���ijɼ�����������������ͼ�����£�
Ƶ�ʷֲ�ͳ�Ʊ� | Ƶ�ʷֲ�ֱ��ͼ | ||
������ | Ƶ�� | Ƶ�� |
|
60��x��70 | 40 | 0.40 | |
70��x��80 | 35 | b | |
80��x��90 | a | 0.15 | |
90��x��100 | 10 | 0.10 | |
�����������Ϣ������������⣺
��1������a�� ��b�� ��
��2���벹ȫƵ���ֲ�ֱ��ͼ��
��3������������ɼ�80�����ϣ���80�֣���Ϊ���㣬��ô�������Ƕ��٣����ҹ����У����ѧ����������������
��1��a��15��b��0.35����2������ͼ����3��25�G��375 �������� �����������1�����ݵ�һ���Ƶ����Ƶ�ʿ�����ܵĵ���������Ȼ����ݵڶ����Ƶ���͵������Ƶ�ʼ������a��b��ֵ�� ��2�����ݣ�1���������aֵ���ɲ�ȫƵ���ֲ�ֱ��ͼ�� ��3��������=������͵������Ƶ��֮�͡�100%�������������������ʣ����㼴�ɵý⣮ ��1���ܵĵ�������=40��0.40=10...

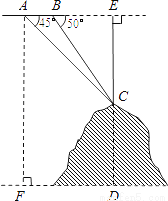

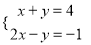 ����2��
����2�� ��
��