题目内容
2.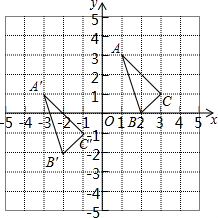 △ABC与△A′B′C′在平面直角坐标系中的位置如图.
△ABC与△A′B′C′在平面直角坐标系中的位置如图.(1)分别写出下列各点的坐标:
A′(-3,1);B′(-2,-2);C′(-1,-1);
(2)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为(a-4,b-2);
(3)求△ABC的面积.
分析 (1)根据平面直角坐标系的特点直接写出坐标;
(2)首先根据A与A′的坐标观察变化规律,P的坐标变换与A点的变换一样,写出点P′的坐标;
(3)先求出△ABC所在的矩形的面积,然后减去△ABC四周的三角形的面积即可.
解答 解:(1)如图所示:
A′(-3,1),B′(-2,-2)、C′(-1,-1);
(2)A(1,3)变换到点A′的坐标是(-3,1),
横坐标减4,纵坐标减2,
∴点P的对应点P′的坐标是(a-4,b-2);
(3)△ABC的面积为:3×2-$\frac{1}{2}$×2×2-$\frac{1}{2}$×3×1-$\frac{1}{2}$×1×1=2.
故答案为:(-3,1),(-2,-2)、(-1,-1);(a-4,b-2).
点评 此题主要考查了平移变换作图,三角形的面积,网格图形中经常利用三角形所在的矩形的面积减去四周三角形的面积的方法求解.

练习册系列答案
相关题目
12.半径为4的圆中,垂直平分一条半径的弦的长是( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
10.下列说法中错误的个数是( )
(1)过一点有且只有一条直线与已知直线平行.
(2)过一点有且只有一条直线与已知直线垂直.
(3)在同一平面内,两条直线的位置关系只有相交、平行两种.
(4)不相交的两条直线叫做平行线.
(5)有公共顶点且有一条公共边的两个角互为邻补角.
(1)过一点有且只有一条直线与已知直线平行.
(2)过一点有且只有一条直线与已知直线垂直.
(3)在同一平面内,两条直线的位置关系只有相交、平行两种.
(4)不相交的两条直线叫做平行线.
(5)有公共顶点且有一条公共边的两个角互为邻补角.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.下列方程一定是一元二次方程的是( )
| A. | (a2+1)x2+bx+c=0 | B. | 5x2-6y-3=0 | C. | ax2-x+2=0 | D. | 3x2+$\frac{2}{x}$-1=0 |
12.若3y-6x=0,则x:y等于( )
| A. | -2:1 | B. | 2:1 | C. | -1:2 | D. | 1:2 |
 (1)在直角坐标系中画出函数y=x2+x-6的图象;
(1)在直角坐标系中画出函数y=x2+x-6的图象;