题目内容
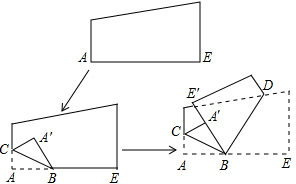如图是一张边被裁直的白纸，把一边折叠后，BC、BD为折痕，A′、E′、B在同一直线上，则∠CBD的度数（ ）| A、不能确定 | B、大于90° |
| C、小于90° | D、等于90° |
考点：翻折变换（折叠问题）
专题：
分析：由折叠的性质，即可得：∠ABC=∠A′BC，∠EBD=∠E′BD，然后由平角的定义，即可求得∠A′BC+∠E′BD=90°，则可求得∠CBD的度数．
解答：解：根据折叠的性质可得：∠ABC=∠A′BC，∠EBD=∠E′BD，
∵∠ABC+∠A′BC+∠E′BD+∠EBD=180°，
∴2∠A′BC+2∠E′BD=180°，
∴∠A′BC+∠E′BD=90°，
∴∠CBD=90°．
故选：D．
∵∠ABC+∠A′BC+∠E′BD+∠EBD=180°，
∴2∠A′BC+2∠E′BD=180°，
∴∠A′BC+∠E′BD=90°，
∴∠CBD=90°．
故选：D．
点评：此题考查了折叠的性质与平角的定义．解题的关键是注意数形结合思想的应用．
练习册系列答案
相关题目
如图，在Rt△ABC中，∠ABC=90°，将Rt△ABC沿直线AB翻折得到△ABF，将Rt△ABC绕点C顺时针方向旋转60°得到△DEC，若点E恰好落在斜边AC上，连接AD．
如图，点E是?ABCD边AD上一点，且AE=