题目内容
1.解方程组:$\left\{\begin{array}{l}x+y=4\\{x^2}+{y^2}-3x+2y=39\end{array}\right.$.分析 先把x+y=4化为x=4-y,再代入二元二次方程,得到关于y的一元二次方程,解方程求出y值,代入x=4-y求出x,得到方程组的解.
解答 解:$\left\{\begin{array}{l}{x+y=4①}\\{{x}^{2}+{y}^{2}-3x+2y=39②}\end{array}\right.$
由①得,x=4-y③
把③代入②得,
2y2-3y-35=0
解得:y1=5,y2=-$\frac{7}{2}$
把y1=5,y2=-$\frac{7}{2}$代入③得,
x1=-1,x2=$\frac{15}{2}$
∴方程组的解为$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{y}_{1}=5}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=\frac{15}{2}}\\{{y}_{2}=-\frac{7}{2}}\end{array}\right.$
点评 本题考查的是二元二次方程组的解法,灵活运用代入法是解题的关键.

练习册系列答案
相关题目
16.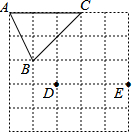 如图是5×5的正方形网格中,以D、E为顶点作位置不同的格点的三角形与△ABC全等,这样格点三角形最多可以画出( )
如图是5×5的正方形网格中,以D、E为顶点作位置不同的格点的三角形与△ABC全等,这样格点三角形最多可以画出( )
 如图是5×5的正方形网格中,以D、E为顶点作位置不同的格点的三角形与△ABC全等,这样格点三角形最多可以画出( )
如图是5×5的正方形网格中,以D、E为顶点作位置不同的格点的三角形与△ABC全等,这样格点三角形最多可以画出( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
13.三角形的三边情况是①a=5,b=12,c=9,②a=15,b=17,c=8,③a=1,b=$2\sqrt{2}$,c=3,④a:b:c=5:12:13,其中直角三角形有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.已知A=5a-3b,B=-6a+4b,则A-B等于( )
| A. | -a+b | B. | 11a+b | C. | 11a-7b | D. | -a-7b |
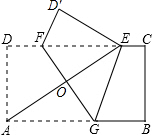 如图,已知矩形纸片ABCD,AD=2,AB=4,将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB,CD交于点G、F、AE与FG交于点O.求证:A,G,E,F四点围成的四边形是菱形.
如图,已知矩形纸片ABCD,AD=2,AB=4,将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB,CD交于点G、F、AE与FG交于点O.求证:A,G,E,F四点围成的四边形是菱形. 如图,Rt△ABC中,直角边是AC、BC,斜边是AB.
如图,Rt△ABC中,直角边是AC、BC,斜边是AB.