题目内容
11．
如图所示，四边形ABCD中，AD∥BC，四边形ABCD的面积为12，求此四边形ABCD四边的中点组成的四边形EFGH的面积．
分析 已知如图，阴影部分面积等于四边形ABCD的面积减去4个空白三角形的面积，可利用相似求得4个空白三角形的面积，进而求解．
解答 解：连接BD，AC
∵E，F，G，H分别为四边形各边中点，
∴△AHE∽△ADB，相似比为$\frac{1}{2}$，面积比为$\frac{1}{4}$，
∴S△ADB=4S△AHE
同理可得，S△ADC=4S△HDG，S△BCD=4S△GCF，S△ACB=4S△EFB
∴S△ADB+S△ADC+S△BCD+S△ACB=2S四边形ABCD=4S△AHE+4S△HDG+4S△GCF+4S△EFB
∴S△AHE+S△HDG+S△GCF+S△EFB=$\frac{1}{2}$S四边形ABCD
∴S四边形EFGH=S四边形ABCD-（S△AHE+S△HDG+S△GCF+S△EFB）=$\frac{1}{2}$S四边形ABCD=$\frac{1}{2}$×12=6．
点评 本题考查了三角形的中位线的性质及相似三角形的性质．三角形中位线定理：三角形的中位线平行于第三边，并且等于第三边的一半．
练习册系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
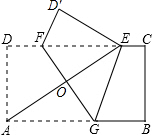如图，已知矩形纸片ABCD，AD=2，AB=4，将纸片折叠，使顶点A与边CD上的点E重合，折痕FG分别与AB，CD交于点G、F、AE与FG交于点O．求证：A，G，E，F四点围成的四边形是菱形．
如图，MN是⊙O的弦，OA⊥MN于A，OA=2，以点A为圆心，OA长为半径作弧交MN于B，点B是AM的中点．
如图，Rt△ABC中，直角边是AC、BC，斜边是AB．