题目内容
9.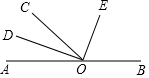 如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°
如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°(1)图中有9个小于平角的角;其中∠COE是∠DOC的余角.
(2)求出∠BOD的度数;
(3)试判断OE是否平分∠BOC,并说明理由.
分析 (1)由过点O的射线有5条即可得出不超过平角的角个数,去除∠AOB后即可得出结论;再由∠DOC+∠COE=90°即可得出∠DOC和∠COE互余;
(2)由平分线的定义结合∠AOC的度数即可求出∠AOD的度数,再根据∠AOD和∠BOD互补即可得出结论;
(3)由∠DOC和∠COE互余即可求出∠COE的度数,再根据∠AOC和∠BOC互补即可求出∠BOC的度数,由∠COE和∠BOC度数间的关系即可得出OE平分∠BOC.
解答 解:(1)∵过点O的射线有5条,
∴小于平角的角的个数为4+3+2=9.
∵∠DOE=∠DOC+∠COE=90°,
∴∠DOC和∠COE互余.
故答案为:9;∠COE.
(2)∵∠AOC=50°,OD平分∠AOC,
∴∠AOD=∠DOC=$\frac{1}{2}$∠AOC=25°,
∴∠BOD=180°-∠AOD=155°.
(3)OE平分∠BOC,理由如下:
∵∠DOC+∠COE=90°,∠DOC=25°,
∴∠COE=65°.
∵∠BOC=180°-∠AOC=130°,
∴∠COE=$\frac{1}{2}$∠BOC.
∴OE平分∠BOC.
点评 本题考查了余角和补角以及角平分线的定义,解题的关键是:(1)根据数角的规则找出小于平角的角的个数;(2)利用角平分线的定义找出∠AOD的度数;(3)求出∠COE和∠BOC度数.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
17.一种长方形地砖,长24厘米,宽16厘米.用这种地砖铺一个正方形,至少需要( )
| A. | 5块 | B. | 8块 | C. | 10块 | D. | 6块 |
1.对于正比例函数y=kx(k≠0),当自变量x的值减小2时,函数y的值减小-6,则k的值为( )
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | 3 | D. | -3 |
18.5月是西安樱桃上市的季节,如果+3吨表示运入仓库的樱桃吨数,那么运出5吨樱桃表示为( )
| A. | -3吨 | B. | +3吨 | C. | -5吨 | D. | +5吨 |
19.用代数式表示“a的3倍与b的差的平方”,正确的是( )
| A. | 3(a-b)2 | B. | 3a-b2 | C. | (a-3b)2 | D. | (3a-b)2 |
 在一次运输任务中,一辆汽车将一批货物从深圳运往广州,到达广州卸货后返回,设汽车从深圳出发x(h)时,汽车与深圳的距离为y(km),y与x的函数关系如图所示.根据图象信息,解答下列问题:
在一次运输任务中,一辆汽车将一批货物从深圳运往广州,到达广州卸货后返回,设汽车从深圳出发x(h)时,汽车与深圳的距离为y(km),y与x的函数关系如图所示.根据图象信息,解答下列问题: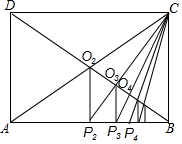 在美国的一堂数学课上,老师给同学们布置了一道“任意等分一条线段”的题.其中有一个学生用了一种与众不同的方法.他在纸上做出了如图所示的一个图形,他以老师给的已知线段AB为一条边作矩形ABCD,设AC、BD交于点O2,作O2P2⊥AB,则垂足P2就是AB的二等分点:连接CP2交BD于点O3,作O3P3⊥AB,则垂足P3就是AB的三等分点;再依次做下去,就得到AB的四等分点,…n等分点.你能用所学过的知识解释其中的缘由吗?
在美国的一堂数学课上,老师给同学们布置了一道“任意等分一条线段”的题.其中有一个学生用了一种与众不同的方法.他在纸上做出了如图所示的一个图形,他以老师给的已知线段AB为一条边作矩形ABCD,设AC、BD交于点O2,作O2P2⊥AB,则垂足P2就是AB的二等分点:连接CP2交BD于点O3,作O3P3⊥AB,则垂足P3就是AB的三等分点;再依次做下去,就得到AB的四等分点,…n等分点.你能用所学过的知识解释其中的缘由吗?