题目内容
2.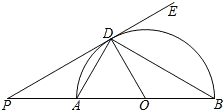 如图,已知AB是⊙O的直径,AD、BD是半圆的弦,∠PDA=∠PBD,∠BDE=60°,若PD=$\sqrt{3}$,则PA的长为1.
如图,已知AB是⊙O的直径,AD、BD是半圆的弦,∠PDA=∠PBD,∠BDE=60°,若PD=$\sqrt{3}$,则PA的长为1.
分析 根据已知可证△AOD为等边三角形,∠P=30°,PA=AD=OA,再证明PD是切线,根据切割线定理即可得出结果.
解答 解:∵AB为直径,
∴∠ADB=90°,
∵∠BDE=60°,
∴∠PDA=180°-90°-60°=30°,
∴∠PBD=∠PDA=30°,
∵OB=OD,
∴∠ODB=∠PBD=30°,
∴∠ADO=60°,
∴△ADO为等边三角形,∠ODP=90°,
∴AD=OA,∠AOD=60°,PD为⊙O的切线,
∴∠P=30°,
∴PA=AD,PD2=PA•PB,
∴($\sqrt{3})$${\;}^{{\;}^{2}}$=PA•3PA
∴PA=1;
故答案为:1.
点评 本题考查了圆周角定理、等边三角形的判定与性质、切线的判定与性质;证明三角形是等边三角形是解决问题的关键.

练习册系列答案
相关题目
12.如图,奥运会徽若忽略文字不看,是轴对称图形的是( )

| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
11.若四边形的对角线互相垂直且相等,则它一定是( )
| A. | 菱形 | B. | 正方形 | ||
| C. | 等腰梯形 | D. | 以上说法均不正确 |
12. 如图,四边形ABCD中,点M、N分别在AB、BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠D的度数为( )
如图,四边形ABCD中,点M、N分别在AB、BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠D的度数为( )
 如图,四边形ABCD中,点M、N分别在AB、BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠D的度数为( )
如图,四边形ABCD中,点M、N分别在AB、BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠D的度数为( )| A. | 115° | B. | 105° | C. | 95° | D. | 85° |
 如图,∠AOC和∠BOD都是直角,如果∠AOB=150°,那么∠COD=30度.
如图,∠AOC和∠BOD都是直角,如果∠AOB=150°,那么∠COD=30度.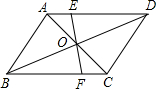 如图,在四边形ABCD中,AD∥BC,对角线AC,BD交于点O,过点O作直线EF交AD于点E,交BC于点F.OE=OF.
如图,在四边形ABCD中,AD∥BC,对角线AC,BD交于点O,过点O作直线EF交AD于点E,交BC于点F.OE=OF.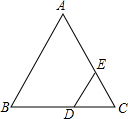 已知:如图,△ABC中,AB=AC,D为BC上一点,过点D作DE∥AB交AC于点E.
已知:如图,△ABC中,AB=AC,D为BC上一点,过点D作DE∥AB交AC于点E.