题目内容
10.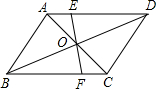 如图,在四边形ABCD中,AD∥BC,对角线AC,BD交于点O,过点O作直线EF交AD于点E,交BC于点F.OE=OF.
如图,在四边形ABCD中,AD∥BC,对角线AC,BD交于点O,过点O作直线EF交AD于点E,交BC于点F.OE=OF.(1)求证:AE=CF.
(2)当EF与BD满足什么位置关系时,四边形BFDE是菱形?请说明理由.
分析 (1)利用平行线的性质结合全等三角形的判定与性质得出即可.
(2)首先得出DO=BO,进而利用对角线互相垂直的平行四边形是菱形求出即可.
解答 (1)证明:∵AD∥BC,
∴∠AEO=∠CFO,
在△AEO和△CFO中
∵$\left\{\begin{array}{l}{∠AEO=∠CFO}\\{EO=FO}\\{∠EOA=∠COF}\end{array}\right.$,
∴△AEO≌△CFO(ASA),
∴AE=CF;
(2)当EF⊥BD时,四边形BFDE是菱形,
理由:由(1)△AEO≌△CFO,同理可得:△DEO≌△BFO,
则DP=BO,
∵EO=FO,∴四边形BFDE是平行四边形,
∵EF⊥BD,∴四边形BFDE是菱形.
点评 此题主要考查了全等三角形的判定与性质以及菱形的判定等知识,得出△AEO≌△CFO是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
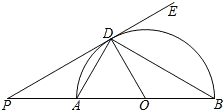 如图,已知AB是⊙O的直径,AD、BD是半圆的弦,∠PDA=∠PBD,∠BDE=60°,若PD=$\sqrt{3}$,则PA的长为1.
如图,已知AB是⊙O的直径,AD、BD是半圆的弦,∠PDA=∠PBD,∠BDE=60°,若PD=$\sqrt{3}$,则PA的长为1.