题目内容
14.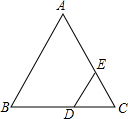 已知:如图,△ABC中,AB=AC,D为BC上一点,过点D作DE∥AB交AC于点E.
已知:如图,△ABC中,AB=AC,D为BC上一点,过点D作DE∥AB交AC于点E.(1)求证:∠C=∠CDE.
(2)若∠A=60°,试判断△DEC的形状,并说明理由.
分析 (1)利用等腰三角形的性质结合平行线的性质得出即可;
(2)利用等边三角形的判定方法,结合△DEC是等腰三角形求出即可.
解答 证明:(1)∵AB=AC,
∴∠B=∠C,
∵DE∥AB,
∴∠CED=∠B,
∴∠C=∠CDE;
(2)△DEC是等边三角形,
理由:∵DE∥AB,
∴∠DEC=∠A=60°,
由(1),△DEC是等腰三角形,
∴△DEC是等边三角形.
点评 此题主要考查了等腰三角形性质和判定以及平行线的性质,得出△DEC是等腰三角形是解题关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
4. 如图,直线AB、CD交于点O,OE平分∠BOC,若∠1=34°,则∠DOE等于( )
如图,直线AB、CD交于点O,OE平分∠BOC,若∠1=34°,则∠DOE等于( )
 如图,直线AB、CD交于点O,OE平分∠BOC,若∠1=34°,则∠DOE等于( )
如图,直线AB、CD交于点O,OE平分∠BOC,若∠1=34°,则∠DOE等于( )| A. | 73° | B. | 90° | C. | 107° | D. | 146° |
3. 如图是一个立体图形的三视图,则这个立体图形是( )
如图是一个立体图形的三视图,则这个立体图形是( )
 如图是一个立体图形的三视图,则这个立体图形是( )
如图是一个立体图形的三视图,则这个立体图形是( )| A. | 圆柱 | B. | 三棱锥 | C. | 圆锥 | D. | 球 |
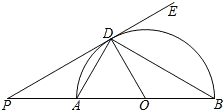 如图,已知AB是⊙O的直径,AD、BD是半圆的弦,∠PDA=∠PBD,∠BDE=60°,若PD=$\sqrt{3}$,则PA的长为1.
如图,已知AB是⊙O的直径,AD、BD是半圆的弦,∠PDA=∠PBD,∠BDE=60°,若PD=$\sqrt{3}$,则PA的长为1. 萧山地铁2号线的开通使银隆百货车流量增大,为方便消费者停车,拟将商场门口某区域边界处有台阶五级,每个台阶高150mm,宽300mm,现把台阶处改建为斜坡以方便汽车出入.为保证不损坏车的底盘,台阶下面设置缓坡带,使斜坡角为5.711°,则台阶下面增加缓坡带的水平宽OA为多少m?(参考tan5.711°≈0.1000,sin5.711°≈0.09951.,cos5.711°≈0.9950)
萧山地铁2号线的开通使银隆百货车流量增大,为方便消费者停车,拟将商场门口某区域边界处有台阶五级,每个台阶高150mm,宽300mm,现把台阶处改建为斜坡以方便汽车出入.为保证不损坏车的底盘,台阶下面设置缓坡带,使斜坡角为5.711°,则台阶下面增加缓坡带的水平宽OA为多少m?(参考tan5.711°≈0.1000,sin5.711°≈0.09951.,cos5.711°≈0.9950)