Question

12．如图，下列图案均是长度相同的火柴按一定的规律拼搭而成：第1个图案需7根火柴，第2个图案需13根火柴，第3个图案需21根火柴，…，依此规律，第6个图案需（　　）根火柴．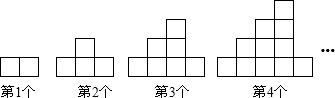

• A． 56
• B． 57
• C． 58
• D． 59

Answer 1

分析 根据第1个图案需7根火柴，7=1×（1+3）+3，第2个图案需13根火柴，13=2×（2+3）+3，第3个图案需21根火柴，21=3×（3+3）+3，得出规律第n个图案需n（n+3）+3根火柴，再把6代入即可求出答案．

解答 解：∵第1个图案需7根火柴，7=1×（1+3）+3，
第2个图案需13根火柴，13=2×（2+3）+3，
第3个图案需21根火柴，21=3×（3+3）+3，
…，
∴第n个图案需n（n+3）+3根火柴，
则第6个图案需：6×（6+3）+3=57（根）；
故选：B．

点评 此题主要考查了图形的变化类，关键是根据题目中给出的图形，通过观察思考，归纳总结出规律，再利用规律解决问题．