题目内容
17.观察一组数 $\frac{1}{3}$,$\frac{2}{5}$,$\frac{3}{7}$,$\frac{4}{9}$,$\frac{5}{11}$,…根据这组数的规律,可推出第100个数是$\frac{100}{201}$.分析 这是一组分数,分子是从1开始的连续自然数,分母是从3开始的连续奇数,且每个分数的分子分母存在的关系:$\frac{分子}{1+2×分子}$,故本题可解.
解答 解:∵分子为1,2,3,4,5,…,
∴第10个数的分子为10,
∵分母为3,5,7,9,11,…
∴第100个数的分母为1+2×100=201,
∴第100个数为:$\frac{100}{201}$,
故答案为:$\frac{100}{201}$
点评 本题是分数找规律的题目,分子是从是连续的自然数,分母是连续的基数,明确这一点问题就容易解决了.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.下列说法正确的是( )
| A. | 0的立方根是0.2 | B. | 4的平方根是±4 | C. | -1的立方根是-1 | D. | -25没有立方根 |
12.如图,下列图案均是长度相同的火柴按一定的规律拼搭而成:第1个图案需7根火柴,第2个图案需13根火柴,第3个图案需21根火柴,…,依此规律,第6个图案需( )根火柴.
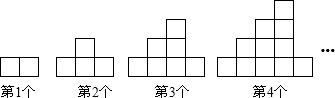

| A. | 56 | B. | 57 | C. | 58 | D. | 59 |
2.5的相反数是( )
| A. | $\frac{1}{5}$ | B. | 5 | C. | -$\frac{1}{5}$ | D. | -5 |
9.用加减消元法解方程组$\left\{\begin{array}{l}{3x-2y=1}\\{3x+y=3}\end{array}\right.$,正确消元后可得方程( )
| A. | 6x-y=4 | B. | 3y=2 | C. | -3y=2 | D. | -y=2 |
 =________.
=________.