题目内容
5. 如图,在矩形ABCD中,AB=3,BC=4,BE⊥AC于E.试求出AC、BE的长.
如图,在矩形ABCD中,AB=3,BC=4,BE⊥AC于E.试求出AC、BE的长.
分析 由在矩形ABCD中,AB=3,BC=4,利用勾股定理即可求得AC的长,然后由三角形的面积公式,求得BE=$\frac{AB•BC}{AC}$,则可求得答案.
解答 解:∵四边形ABCD是矩形,
∴∠ABC=90°,
∵AB=3,BC=4,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5,
∵BE⊥AC,
∴S△ABC=$\frac{1}{2}$AB•BC=$\frac{1}{2}$AC•BE,
∴BE=$\frac{AB•BC}{AC}$=$\frac{12}{5}$.
点评 此题考查了矩形的性质以及勾股定理.注意直角三角形斜边上的高等于直角边相乘除以斜边.

练习册系列答案
相关题目
14.若|a|=8,则a的值是( )
| A. | -8 | B. | 8 | C. | ±8 | D. | ±$\frac{1}{8}$ |
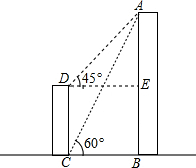 如图,AB、CD为两栋建筑物,建筑物CD的高度为20m,从建筑物CD的顶部D点测得建筑物AB的顶部A点的仰角为45°,从建筑物CD的底部C点测得建筑物AB的顶部A点的仰角60°,求建筑物AB的高度(结果保留整数)(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,AB、CD为两栋建筑物,建筑物CD的高度为20m,从建筑物CD的顶部D点测得建筑物AB的顶部A点的仰角为45°,从建筑物CD的底部C点测得建筑物AB的顶部A点的仰角60°,求建筑物AB的高度(结果保留整数)(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73) 如图,已知点A、B、C在⊙O上,且AB=AC,∠BAC=40°,BD为⊙O的直径,则∠ADB=70°.
如图,已知点A、B、C在⊙O上,且AB=AC,∠BAC=40°,BD为⊙O的直径,则∠ADB=70°. 如图,正方形ABCD的边长为1cm,以CD为直径在正方形内画半圆,再以C为圆心,1cm长为半径画弧BD,则图中阴影部分的面积为$\frac{π}{8}$cm2.
如图,正方形ABCD的边长为1cm,以CD为直径在正方形内画半圆,再以C为圆心,1cm长为半径画弧BD,则图中阴影部分的面积为$\frac{π}{8}$cm2.