题目内容
3. 如图,AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,且S△ABC=7,DE=2,AB=4,求AC的长.
如图,AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,且S△ABC=7,DE=2,AB=4,求AC的长.
分析 根据角平分线性质求出DF,根据三角形面积公式求出△ABD的面积,求出△ADC面积,即可求出答案.
解答 解:∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC于点F,
∴DE=DF=2,
∵S△ADB=$\frac{1}{2}$AB×DE=$\frac{1}{2}$×4×2=4,
∵△ABC的面积为7,
∴△ADC的面积为7-4=3,
∴$\frac{1}{2}$AC×DF=3,
∴$\frac{1}{2}$AC×2=3,
∴AC=3.
点评 本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.

练习册系列答案
相关题目
11. 在数轴上表示a、b两个实数的点的位置如图所示,则化简|a-b|-|a+b|的结果为( )
在数轴上表示a、b两个实数的点的位置如图所示,则化简|a-b|-|a+b|的结果为( )
 在数轴上表示a、b两个实数的点的位置如图所示,则化简|a-b|-|a+b|的结果为( )
在数轴上表示a、b两个实数的点的位置如图所示,则化简|a-b|-|a+b|的结果为( )| A. | a | B. | 2b | C. | 2a-2b | D. | -2b |
18. 如图,△ABC中,∠BAC=80°,AB、AC的垂直平分线交于点O,则∠BOC=( )
如图,△ABC中,∠BAC=80°,AB、AC的垂直平分线交于点O,则∠BOC=( )
 如图,△ABC中,∠BAC=80°,AB、AC的垂直平分线交于点O,则∠BOC=( )
如图,△ABC中,∠BAC=80°,AB、AC的垂直平分线交于点O,则∠BOC=( )| A. | 100° | B. | 130° | C. | 160° | D. | 150° |
8.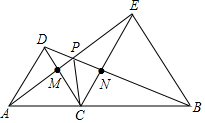 如图,△DAC和△EBC均是等边三角形,AE交BD于P点,AE、BD分别与CD、CE交于点M、N,且A、C、B在同一直线上,有如下结论:①△ACE≌△DCB;②CM=CN;③∠APD=60°;④∠APC=60°,其中正确个数是( )
如图,△DAC和△EBC均是等边三角形,AE交BD于P点,AE、BD分别与CD、CE交于点M、N,且A、C、B在同一直线上,有如下结论:①△ACE≌△DCB;②CM=CN;③∠APD=60°;④∠APC=60°,其中正确个数是( )
 如图,△DAC和△EBC均是等边三角形,AE交BD于P点,AE、BD分别与CD、CE交于点M、N,且A、C、B在同一直线上,有如下结论:①△ACE≌△DCB;②CM=CN;③∠APD=60°;④∠APC=60°,其中正确个数是( )
如图,△DAC和△EBC均是等边三角形,AE交BD于P点,AE、BD分别与CD、CE交于点M、N,且A、C、B在同一直线上,有如下结论:①△ACE≌△DCB;②CM=CN;③∠APD=60°;④∠APC=60°,其中正确个数是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
13.设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=-(x+1)2+k上的三点,则y1,y2,y3的大小关系为( )
| A. | y1>y2>y3 | B. | y1>y3>y2 | C. | y2>y3>y1 | D. | y3>y1>y2 |
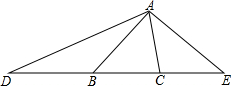 如图,已知:∠ABC=50°,∠ACB=80°,点D、B、C、E四点共线,DB=AB,CE=CA,求∠D、∠E、∠DAE的度数.
如图,已知:∠ABC=50°,∠ACB=80°,点D、B、C、E四点共线,DB=AB,CE=CA,求∠D、∠E、∠DAE的度数.