题目内容
4.如图,反比例函数y=$\frac{k}{x}$(k≠0,x>0)的图象与直线y=3x相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.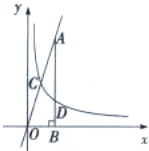
(1)求k的值;
(2)求点C的坐标;
(3)在y轴上确定一点M,使点M到C、D两点距离之和d=MC+MD最小,求点M的坐标.
分析 (1)根据A坐标,以及AB=3BD求出D坐标,代入反比例解析式求出k的值;
(2)直线y=3x与反比例解析式联立方程组即可求出点C坐标;
(3)作C关于y轴的对称点C′,连接C′D交y轴于M,则d=MC+MD最小,得到C′(-$\frac{\sqrt{3}}{3}$,$\sqrt{3}$),求得直线C′D的解析式为y=-$\sqrt{3}$x+1+$\sqrt{3}$,直线与y轴的交点即为所求.
解答 解:(1)∵A(1,3),
∴AB=3,OB=1,
∵AB=3BD,
∴BD=1,
∴D(1,1)
将D坐标代入反比例解析式得:k=1;
(2)由(1)知,k=1,
∴反比例函数的解析式为;y=$\frac{1}{x}$,
解:$\left\{\begin{array}{l}{y=3x}\\{y=\frac{1}{x}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{\sqrt{3}}{3}}\\{y=\sqrt{3}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{\sqrt{3}}{3}}\\{y=-\sqrt{3}}\end{array}\right.$,
∵x>0,
∴C($\frac{\sqrt{3}}{3}$,$\sqrt{3}$);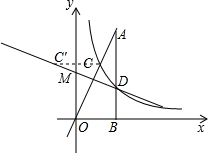
(3)如图,作C关于y轴的对称点C′,连接C′D交y轴于M,则d=MC+MD最小,
∴C′(-$\frac{\sqrt{3}}{3}$,$\sqrt{3}$),
设直线C′D的解析式为:y=kx+b,
∴$\left\{\begin{array}{l}{\sqrt{3}=-\frac{\sqrt{3}}{3}k+b}\\{1=k+b}\end{array}\right.$,∴$\left\{\begin{array}{l}{k=3-2\sqrt{3}}\\{b=-2+2\sqrt{3}}\end{array}\right.$,
∴y=(3-2$\sqrt{3}$)x+2$\sqrt{3}$-2,
当x=0时,y=2$\sqrt{3}$-2,
∴M(0,2$\sqrt{3}$-2).
点评 此题考查了反比例函数与一次函数的交点问题,涉及的知识有:坐标与图形性质,待定系数法确定函数解析式,以及直线与反比例的交点求法,熟练掌握待定系数法是解本题的关键.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案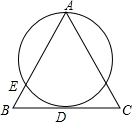 如图,在△ABC中,AB=AC,D是边BC的中点,一个圆过点A,交边AB于点E,且与BC相切于点D,则该圆的圆心是( )
如图,在△ABC中,AB=AC,D是边BC的中点,一个圆过点A,交边AB于点E,且与BC相切于点D,则该圆的圆心是( )| A. | 线段AE的中垂线与线段AC的中垂线的交点 | |
| B. | 线段AB的中垂线与线段AC的中垂线的交点 | |
| C. | 线段AE的中垂线与线段BC的中垂线的交点 | |
| D. | 线段AB的中垂线与线段BC的中垂线的交点 |
 若关于x的二次函数y=ax2+bx+c(a>0,c>0,a,b,c是常数)与x轴交于两个不同的点A(x1,0),B(x2,0)(0<x1<x2),与y轴交于点P,其图象顶点为点M,点O为坐标原点.
若关于x的二次函数y=ax2+bx+c(a>0,c>0,a,b,c是常数)与x轴交于两个不同的点A(x1,0),B(x2,0)(0<x1<x2),与y轴交于点P,其图象顶点为点M,点O为坐标原点.
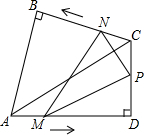 如图,在同一平面上,两块斜边相等的直角三角板Rt△ABC和Rt△ADC拼在一起,使斜边AC完全重合,且顶点B,D分别在AC的两旁,∠ABC=∠ADC=90°,∠CAD=30°,AB=BC=4cm
如图,在同一平面上,两块斜边相等的直角三角板Rt△ABC和Rt△ADC拼在一起,使斜边AC完全重合,且顶点B,D分别在AC的两旁,∠ABC=∠ADC=90°,∠CAD=30°,AB=BC=4cm