题目内容
13.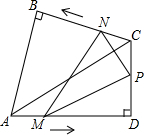 如图,在同一平面上,两块斜边相等的直角三角板Rt△ABC和Rt△ADC拼在一起,使斜边AC完全重合,且顶点B,D分别在AC的两旁,∠ABC=∠ADC=90°,∠CAD=30°,AB=BC=4cm
如图,在同一平面上,两块斜边相等的直角三角板Rt△ABC和Rt△ADC拼在一起,使斜边AC完全重合,且顶点B,D分别在AC的两旁,∠ABC=∠ADC=90°,∠CAD=30°,AB=BC=4cm(1)填空:AD=2$\sqrt{6}$(cm),DC=2$\sqrt{2}$(cm)
(2)点M,N分别从A点,C点同时以每秒1cm的速度等速出发,且分别在AD,CB上沿A→D,C→B方向运动,当N点运动到B点时,M、N两点同时停止运动,连接MN,求当M、N点运动了x秒时,点N到AD的距离(用含x的式子表示)
(3)在(2)的条件下,取DC中点P,连接MP,NP,设△PMN的面积为y(cm2),在整个运动过程中,△PMN的面积y存在最大值,请求出y的最大值.
(参考数据sin75°=$\frac{\sqrt{6}+\sqrt{2}}{4}$,sin15°=$\frac{\sqrt{6}-\sqrt{2}}{4}$)
分析 (1)由勾股定理求出AC,由∠CAD=30°,得出DC=$\frac{1}{2}$AC=2$\sqrt{2}$,由三角函数求出AD即可;
(2)过N作NE⊥AD于E,作NF⊥DC,交DC的延长线于F,则NE=DF,求出∠NCF=75°,∠FNC=15°,由三角函数求出FC,得NE=DF=$\frac{\sqrt{6}-\sqrt{2}}{4}$x+2$\sqrt{2}$,即可得出结果;
(3)由三角函数求出FN,得出PF,△PMN的面积y=梯形MDFN的面积-△PMD的面积-△PNF的面积,得出y是x的二次函数,即可得出y的最大值.
解答 解:(1)∵∠ABC=90°,AB=BC=4cm,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,
∵∠ADC=90°,∠CAD=30°,
∴DC=$\frac{1}{2}$AC=2$\sqrt{2}$,
∴AD=$\sqrt{3}$DC=2$\sqrt{6}$;
故答案为:2$\sqrt{6}$,2$\sqrt{2}$;
(2)过点N作NE⊥AD于E,作NF⊥DC,交DC的延长线于F,如图所示: 则NE=DF,
则NE=DF,
∵∠ABC=∠ADC=90°,AB=BC,∠CAD=30°,
∴∠ACB=45°,∠ACD=60°,
∴∠NCF=180°-45°-60°=75°,∠FNC=15°,
∵sin∠FNC=$\frac{FC}{NC}$,NC=x,
∴FC=$\frac{\sqrt{6}-\sqrt{2}}{4}$x,
∴NE=DF=$\frac{\sqrt{6}-\sqrt{2}}{4}$x+2$\sqrt{2}$,
∴点N到AD的距离为$\frac{\sqrt{6}-\sqrt{2}}{4}$x+2$\sqrt{2}$;
(3)∵sin∠NCF=$\frac{FN}{NC}$,
∴FN=$\frac{\sqrt{6}+\sqrt{2}}{4}$x,
∵P为DC的中点,
∴PD=CP=$\sqrt{2}$,
∴PF=$\frac{\sqrt{6}-\sqrt{2}}{4}$x+$\sqrt{2}$,
∴△PMN的面积y=梯形MDFN的面积-△PMD的面积-△PNF的面积
=$\frac{1}{2}$($\frac{\sqrt{6}+\sqrt{2}}{4}$x+2$\sqrt{6}$-x)($\frac{\sqrt{6}-\sqrt{2}}{4}$x+2$\sqrt{2}$)-$\frac{1}{2}$(2$\sqrt{6}$-x)×$\sqrt{2}$-$\frac{1}{2}$($\frac{\sqrt{6}-\sqrt{2}}{4}$x+$\sqrt{2}$)($\frac{\sqrt{6}+\sqrt{2}}{4}$x)
=$\frac{\sqrt{2}-\sqrt{6}}{8}$x2+$\frac{7-\sqrt{3}-2\sqrt{2}}{4}$x+2$\sqrt{3}$,
即y是x的二次函数,
∵$\frac{\sqrt{2}-\sqrt{6}}{8}$<0,
∴y有最大值,
当x=-$\frac{\frac{7-\sqrt{3}-2\sqrt{2}}{4}}{2×\frac{\sqrt{2}-\sqrt{6}}{8}}$=$\frac{7-\sqrt{3}-2\sqrt{2}}{\sqrt{6}-\sqrt{2}}$时,
y有最大值为$\frac{6\sqrt{6}+7\sqrt{3}-10\sqrt{2}-30}{4\sqrt{2}-4\sqrt{6}}$=$\frac{8\sqrt{3}+23\sqrt{6}+9\sqrt{2}-16}{16}$.
点评 本题是相似形综合题目,考查了勾股定理、三角函数、三角形面积的计算、二次函数的最值、等腰直角三角形的性质等知识;本题难度较大,综合性强,特别是(2)(3)中,需要通过作辅助线运用三角函数和二次函数才能得出结果.

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案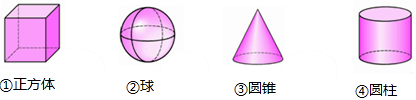
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ③④ |
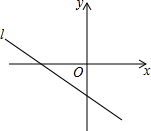 如图,直线l:y=-$\frac{2}{3}$x-3与直线y=a(a为常数)的交点在第四象限,则a可能在( )
如图,直线l:y=-$\frac{2}{3}$x-3与直线y=a(a为常数)的交点在第四象限,则a可能在( )| A. | 1<a<2 | B. | -2<a<0 | C. | -3≤a≤-2 | D. | -10<a<-4 |
| A. | -1 | B. | -2 | C. | 0 | D. | 1 |
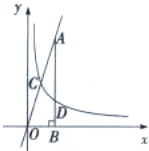
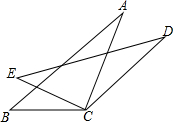 如图,CA=CD,∠B=∠E,∠BCE=∠ACD.求证:AB=DE.
如图,CA=CD,∠B=∠E,∠BCE=∠ACD.求证:AB=DE.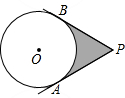 如图,P为⊙O外一点,PA,PB是⊙O的切线,A,B为切点,PA=$\sqrt{3}$,∠P=60°,则图中阴影部分的面积为$\sqrt{3}$-$\frac{1}{3}$π.
如图,P为⊙O外一点,PA,PB是⊙O的切线,A,B为切点,PA=$\sqrt{3}$,∠P=60°,则图中阴影部分的面积为$\sqrt{3}$-$\frac{1}{3}$π.