题目内容
已知关于x的方程16x2-kx+9=0有两个相等的实数根，求k的值和方程的根．
考点：根的判别式
专题：
分析：根据方程16x2-kx+9=0有两个相等的实数根，所以根的判别式△=b2-4ac=k2-4×16×9=0，然后解方程即可得到k的值，再把k的值代入方程，解方程即可．
解答：解：∵方程16x2-kx+9=0有两个相等的实数根，
∴△=k2-4×16×9=0，
∴k=±24．
当k=24时，方程16x2-24x+9=0的解为x1=x2=
；
当k=-24时，方程16x2+24x+9=0的解为x1=x2=-
．
∴△=k2-4×16×9=0，
∴k=±24．
当k=24时，方程16x2-24x+9=0的解为x1=x2=
| 3 |
| 4 |
当k=-24时，方程16x2+24x+9=0的解为x1=x2=-
| 3 |
| 4 |
点评：本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的根判别式以及一元二次方程的解法，△=b2-4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．
练习册系列答案
相关题目
如图图案中既是轴对称图形又是中心对称图形的是（ ）
A、 |
B、 |
C、 |
D、 |
已知跷跷板AB长3m，由于跷跷板的支撑点O偏离中点，所以当A端碰到地面时，AB与地面的夹角为α（如图①），当B端碰到地面时，AB与地面的夹角为β（如图②），则跷跷板AB的支撑点O到地面的高度OH用含α、β的式子表示正确的是（ ）
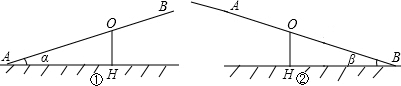
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图所示，AB∥CD，EF∥GH，CD与EF相交于点I，试探究∠1与∠2的关系，并说明理由．无论a，b为何值，代数式a2+b2+4b+5-2a的值总是（ ）
| A、非负数 | B、0 | C、正数 | D、负数 |
下列各组整式中不是同类项的是（ ）
| A、3m2n和2m2n | ||
B、2xy2与
| ||
| C、-5ab与-6ab | ||
| D、a与3a |
