题目内容
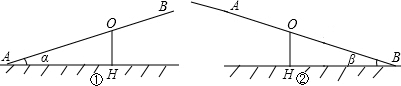
已知跷跷板AB长3m,由于跷跷板的支撑点O偏离中点,所以当A端碰到地面时,AB与地面的夹角为α(如图①),当B端碰到地面时,AB与地面的夹角为β(如图②),则跷跷板AB的支撑点O到地面的高度OH用含α、β的式子表示正确的是( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:解直角三角形的应用
专题:
分析:根据三角函数的知识分别用OH表示出AO,BO的长,再根据不等臂跷跷板AB长4m,即可列出方程求解即可.
解答:解:依题意有:AO=OH÷sinα,BO=OH÷sinβ,
AO+BO=OH÷sinα+OH÷sinβ,即OH÷sinα+OH÷sinβ=3m,
则OH=
m.
故选C.
AO+BO=OH÷sinα+OH÷sinβ,即OH÷sinα+OH÷sinβ=3m,
则OH=
| 3sinαsinβ |
| sinα+sinβ |
故选C.
点评:本题考查的是解直角三角形的应用,根据题意利用锐角三角函数的定义求解是解答此题的关键.

练习册系列答案
相关题目
一元二次方程x2=1的情况是( )
| A、有两个不相等的实数根 |
| B、有两个相等的实数根 |
| C、只有一个实数根 |
| D、没有实数根 |
21,24,30,24,21,x这组数据的平均数为24,则这组数据的众数是( )
| A、21 | B、22 | C、24 | D、30 |
一天有24小时,一小时有60分,一分为60秒.故一天共有86400秒.用科学记数法表示86400为( )
| A、8.64×104 |
| B、8.64×105 |
| C、0.864×105 |
| D、0.864×104 |
 如图,这是两块相同的三角板拼成的一个图形,BC边与DF边在同一条直线上.请找出图中的一组平行线,并说明你的理由.
如图,这是两块相同的三角板拼成的一个图形,BC边与DF边在同一条直线上.请找出图中的一组平行线,并说明你的理由. 美化城市,改善人们的居住环境已成为城市建设的一项重要内容,某市城区近几年来,通过拆旧房.植草,栽树,修建公园等设施,使城区绿地面积不断增加(如图所示).
美化城市,改善人们的居住环境已成为城市建设的一项重要内容,某市城区近几年来,通过拆旧房.植草,栽树,修建公园等设施,使城区绿地面积不断增加(如图所示).