题目内容
11．已知A（m，1），B（m+1，2）是反比例函数y=$\frac{m}{x}$（m≠0）图象上两点，抛物线y=x2-2mx-2m+1与直线y=2的交点的横坐标是（ ）| A． | 3或-1 | B． | -3或-1 | C． | -3或1 | D． | 3或1 |
分析 先根据题意得出m的值，再把m的值代入抛物线的解析式，进而可得出结论．
解答 解：∵A（m，1），B（m+1，2）是反比例函数y=$\frac{m}{x}$（m≠0）图象上两点，
∴m=2（m+1），解得m=-2，
∴抛物线y=x2-2mx-2m+1的解析式为：y=x2+4x+5，
∴当y=2时，即x2+4x+5=2，解得x=-1或x=-3．
故选B．
点评 本题考查的是反比例函数图象上点的坐标特点，熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．
练习册系列答案
相关题目
如图，AD是Rt△ABC斜边上的高．若AB=4cm，BC=10cm，则BD=1.6cm．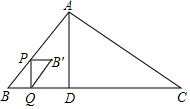
如图，在△ABC中，AD⊥BC于点D，BD=3cm，DC=8cm，AD=4cm，动点P从点B出发，沿折线BA-AC向终点C做匀速运动，点P在线段BA上的运动速度是5cm/s；在线段AC上的运动速度是$\sqrt{5}$cm/s，当点P不与点B、C重合时，过点P作PQ⊥BC于点Q，将△PBQ绕PQ的中点旋转180°得到△QB′P，设四边形PBQB′与△ABD重叠部分图形的面积为y（cm2），点P的运动时间为x（s）．
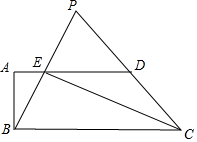已知：如图，在梯形ABCD中，AD∥BC，∠ABC=90°，AB=4，AD=8，sin∠BCD=$\frac{4}{5}$，CE平分∠BCD，交边AD于点E，联结BE并延长，交CD的延长线于点P．
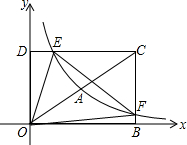如图，在平面直角坐标系中，已知四边形DOBC是矩形，且D（0，2），B（3，0）．若反比例函数y=-$\frac{{k}_{1}}{x}$（x＞0）的图象经过线段OC的中点A，交DC于点E，交BC于点F，设直线EF的解析式为y=k2x+b．