题目内容
6.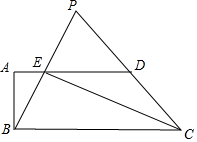 已知:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,AB=4,AD=8,sin∠BCD=$\frac{4}{5}$,CE平分∠BCD,交边AD于点E,联结BE并延长,交CD的延长线于点P.
已知:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,AB=4,AD=8,sin∠BCD=$\frac{4}{5}$,CE平分∠BCD,交边AD于点E,联结BE并延长,交CD的延长线于点P.(1)求梯形ABCD的周长;
(2)求PE的长.
分析 (1)过D作DF⊥BC于F,根据矩形的性质得到DF=AB=4,BF=AD=8,根据三角函数的定义得到CD=5,于是得到结论;
(2)根据平行线的性质得到∠DEC=∠BCE,根据角平分线的定义得到∠DCE=∠BCE,等量代换得到∠DEC=∠DCE,于是得到DE=CD=5,由勾股定理得到BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=5,根据相似三角形的性质即可得到结论.
解答  解:(1)过D作DF⊥BC于F,
解:(1)过D作DF⊥BC于F,
则四边形ABFD是矩形,
∴DF=AB=4,BF=AD=8,
∵sin∠BCD=$\frac{DF}{CD}$=$\frac{4}{5}$,
∴CD=5,
∴CF=3,
∴梯形ABCD的周长=4+8+3+5+8=28;
(2)∵AD∥BC,
∴∠DEC=∠BCE,
∵CE平分∠BCD,
∴∠DCE=∠BCE,
∴∠DEC=∠DCE,
∴DE=CD=5,
∴AE=3,
∴BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=5,
∵DE∥BC,
∴△PED∽△PBC,
∴$\frac{PE}{PB}=\frac{DE}{BC}$,
即$\frac{PE}{PE+5}=\frac{5}{11}$,
∴PE=$\frac{25}{6}$.
点评 本题考查了相似三角形的判定和性质.平行线的性质,角平分线的定义,等腰三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知A(m,1),B(m+1,2)是反比例函数y=$\frac{m}{x}$(m≠0)图象上两点,抛物线y=x2-2mx-2m+1与直线y=2的交点的横坐标是( )
| A. | 3或-1 | B. | -3或-1 | C. | -3或1 | D. | 3或1 |

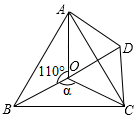 如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕着点C按顺时针方向旋转60°得到△ADC,连结OD,当α=150°时,△AOD是直角三角形.
如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕着点C按顺时针方向旋转60°得到△ADC,连结OD,当α=150°时,△AOD是直角三角形. 已知,甲地到乙地的路程为260千米,一辆大货车从甲地前往乙地运送物资,行驶2小时在途中某地出现故障,立即通知技术人员乘小汽车从甲地赶来维修(通知时间忽略不计),小汽车到达该地后经过20分钟修好大货车后以原速原路返回甲地,同时大货车以原来1.5倍的速度前往乙地,如图是两车距甲地的路程y(千米)与大货车所用时间x(小时)之间的函数图象,则大货车到达乙地比小汽车返回甲地晚2$\frac{1}{6}$小时.
已知,甲地到乙地的路程为260千米,一辆大货车从甲地前往乙地运送物资,行驶2小时在途中某地出现故障,立即通知技术人员乘小汽车从甲地赶来维修(通知时间忽略不计),小汽车到达该地后经过20分钟修好大货车后以原速原路返回甲地,同时大货车以原来1.5倍的速度前往乙地,如图是两车距甲地的路程y(千米)与大货车所用时间x(小时)之间的函数图象,则大货车到达乙地比小汽车返回甲地晚2$\frac{1}{6}$小时. 如图,已知E点在正方形ABCD的BC边的延长线上,且CE=AC,AE与CD相交于点F,则∠AFC=112.5°.
如图,已知E点在正方形ABCD的BC边的延长线上,且CE=AC,AE与CD相交于点F,则∠AFC=112.5°.