题目内容
(本题满分12分)在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.

(1)如图1,若点D与圆心O重合,AC=2,求⊙O的半径r;
(2)如图2,若点D与圆心O不重合,∠BAC=25°,求∠DCA的度数.
(1) ;(2)40°.
;(2)40°.
【解析】
试题分析:(1)过点O作OE⊥AC于E,根据垂径定理可得AE= AC,再根据翻折的性质可得OE=
AC,再根据翻折的性质可得OE= ,然后在Rt△AOE中,利用勾股定理列式计算即可得解;
,然后在Rt△AOE中,利用勾股定理列式计算即可得解;
(2)连接BC,根据直径所对的圆周角是直角求出∠ACB,根据直角三角形两锐角互余求出∠B,再根据翻折的性质得到 所对的圆周角,然后根据∠ACD等于
所对的圆周角,然后根据∠ACD等于 所对的圆周角减去
所对的圆周角减去 所对的圆周角,计算即可得解.
所对的圆周角,计算即可得解.
试题解析:(1)如图,过点O作OE⊥AC于E,
则AE= AC=
AC= ,
,
∵翻折后点D与圆心O重合,∴OE= ,
,
在Rt△AOE中, ,即
,即 ,解得
,解得 ;
;
(2)连接BC,
∵AB是直径,∴∠ACB=90°,
∵∠BAC=25°,∴∠B=90°﹣∠BAC=90°﹣25°=65°,
根据翻折的性质, 所对的圆周角为∠B,
所对的圆周角为∠B, 所对的圆周角为∠ADC,
所对的圆周角为∠ADC,
∴∠ADC+∠B=180°,∴∠B=∠CDB=65°,∴∠DCA=∠CDB﹣∠A=65°﹣25°=40°.

考点:1.垂径定理;2.含30度角的直角三角形;3.圆周角定理;4.翻折变换(折叠问题).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目





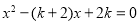 .
. 取何值时,这个方程一定有实数根;
取何值时,这个方程一定有实数根; ,另两边长
,另两边长 、
、 恰好是这个方程的两个根 ,求△ABC的周长.
恰好是这个方程的两个根 ,求△ABC的周长.