题目内容
已知关于x的一元二次方程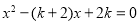 .
.
(1)试说明无论 取何值时,这个方程一定有实数根;
取何值时,这个方程一定有实数根;
(2)若等腰△ABC的一边长 ,另两边长
,另两边长 、
、 恰好是这个方程的两个根 ,求△ABC的周长.
恰好是这个方程的两个根 ,求△ABC的周长.
(1)证明见解析;(2)5.
【解析】
试题分析:(1)根据方程表示出根的判别式,利用完全平方公式变形后,根据非负数的性质确定出根的判别式大于等于0,且为完全平方式,即可得证;
(2)分a为腰与a为底两种情况,求出方程的解确定出b与c,即可求出周长.
试题解析:(1)方程x2-(k+2)x+2k=0,
∵△=(k+2)2-8k=(k-2)2≥0,
∴无论k取何值时,这个方程总有实数根,并且有有理根;
(2)若a=1是腰,则x=1为已知方程的解,
将x=1代入方程得:k=1,即方程为x2-3x+2=0,
解得:x=1或x=2,
此时三角形三边为1,1,2,不合题意,舍去;
若a=1是底时,b=c为腰,即k=2,方程为x2-4x+4=0,
解得:x1=x2=2,
此时b=c=2,即三角形三边长为1,2,2,周长为1+2+2=5.
考点:1.根的判别式;2.根与系数的关系;3.等腰三角形的性质.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
 的方程
的方程 的两根互为倒数,则
的两根互为倒数,则 .
.


 ).
).
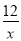 (x>0)图象上任意一点,以P为圆心,PO为半径的圆与坐标轴分别交于点A、B.
(x>0)图象上任意一点,以P为圆心,PO为半径的圆与坐标轴分别交于点A、B.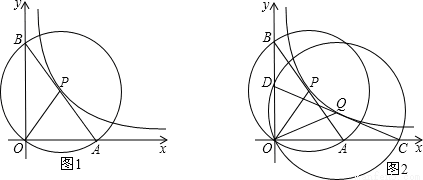
 ,
,  中,单项式的个数有 个
中,单项式的个数有 个