题目内容
6.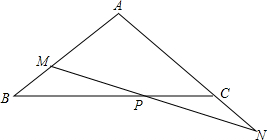 如图,已知在△ABC中,AB=AC,P是BC边上的-点,过点P引直线分别交AB于点M,交AC的延长线于点N,且PM=PN.
如图,已知在△ABC中,AB=AC,P是BC边上的-点,过点P引直线分别交AB于点M,交AC的延长线于点N,且PM=PN.(1)写出图中除AB和AC,PM和PN外的其他相等的线段.
(2)证明你的结论.
分析 (1)观察图形可猜想BM=CN;
(2)过点M作MD∥AC与BC交于点D,易证△PMD≌△PNC,则MD=CN,由AB=AC和MD∥AC可证∠B=∠MDB,根据等角对等边可得证结论.
解答 解:(1)BM=CN;
(2)过点M作MD∥AC与BC交于点D,
∴∠MDC=∠NCD,
在△PMD和△PNC中,
$\left\{\begin{array}{l}{∠MDC=∠NCD}\\{∠DPM=∠CPN}\\{PM=PN}\end{array}\right.$,
∴△PMD≌△PNC,
∴MD=CN,
∵AB=AC,
∴∠B=∠ACB,
∵MD∥AC,
∴∠MDB=∠ACB,
∴∠B=∠MDB,
∴BM=MD,
∴BM=CN.
点评 本题主要考查了全等三角形的判定与性质、等腰三角形的判定与性质、平行线的性质,熟练掌握全等三角形的判定方法是解决问题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
16.下列一元二次方程中,没有实根的是( )
| A. | x2+2x-3=0 | B. | x2+x+$\frac{1}{4}$=0 | C. | x2+$\sqrt{2}$x+1=0 | D. | -x2+3=0 |
11.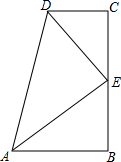 如图所示,在四边形ABCD中,∠B=∠C=90°,DE平分∠ADC,AE平分∠BAD,E在BC上,下列结论不成立的是( )
如图所示,在四边形ABCD中,∠B=∠C=90°,DE平分∠ADC,AE平分∠BAD,E在BC上,下列结论不成立的是( )
 如图所示,在四边形ABCD中,∠B=∠C=90°,DE平分∠ADC,AE平分∠BAD,E在BC上,下列结论不成立的是( )
如图所示,在四边形ABCD中,∠B=∠C=90°,DE平分∠ADC,AE平分∠BAD,E在BC上,下列结论不成立的是( )| A. | E是BC的中点 | B. | CD+AB=AD | C. | ∠AED=90° | D. | CE+DE=BC |
18.购一批水果,运输过程中损失10%,不计其他费用,要想获得至少20%的利润,则售价至少比进价提高 ( )
| A. | 34% | B. | 33.4% | C. | 33.3% | D. | 33% |
 如图所示,△ABC≌△DFE.试求∠FDB+∠ABD的值.
如图所示,△ABC≌△DFE.试求∠FDB+∠ABD的值.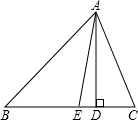 如图,在△ABC中,AD是边BC上的高,AE是∠A的角平分线,且∠C=60°,∠B=40°,求∠AED,∠EAD,∠CAD的度数.
如图,在△ABC中,AD是边BC上的高,AE是∠A的角平分线,且∠C=60°,∠B=40°,求∠AED,∠EAD,∠CAD的度数. 已知AB,CD相交于点O,且AB=CD,AD=CB,
已知AB,CD相交于点O,且AB=CD,AD=CB,