题目内容
3.在同一时刻物体的高度与它的影长成正比例,在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为90米,那么高楼的高度是多少米?分析 设此高楼的高度为h米,再根据同一时刻物高与影长成正比列出关于h的比例式,求出h的值即可.
解答 解:设此高楼的高度为h米,
∵在同一时刻,有人测得一高为1.8米得竹竿的影长为3米,某高楼的影长为60米,
∴$\frac{1.8}{3}$=$\frac{h}{90}$,
解得h=54.
答:高楼的高度是54米.
点评 本题考查的是相似三角形的应用,熟知同一时刻物高与影长成正比是解答此题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
18.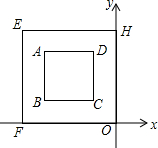 如图,在直角坐标系中,正方形EFOH是正方形ABCD经过位似变换得到的,对角线OE=4,则位似中心的坐标是( )
如图,在直角坐标系中,正方形EFOH是正方形ABCD经过位似变换得到的,对角线OE=4,则位似中心的坐标是( )
 如图,在直角坐标系中,正方形EFOH是正方形ABCD经过位似变换得到的,对角线OE=4,则位似中心的坐标是( )
如图,在直角坐标系中,正方形EFOH是正方形ABCD经过位似变换得到的,对角线OE=4,则位似中心的坐标是( )| A. | (-2,2) | B. | (-$\sqrt{2}$,$\sqrt{2}$) | C. | (-4,4) | D. | (0,0) |
8.若函数y=(2m+1)x2+(1-2m)x+1(m为常数)是一次函数,则m的值为( )
| A. | m$>\frac{1}{2}$ | B. | m=$\frac{1}{2}$ | C. | m$<\frac{1}{2}$ | D. | m=-$\frac{1}{2}$ |
15.已知△ABC的面积是1,A1、B1、C1分别是△ABC三边上的中点,△A1B1C1的面积记为S1;A2、B2、C2分别是△A1B1C1三边上的中点,△A2B2C2的面积记为S2;以此类推,则△A4B4C4的面积S4是( )
| A. | $\frac{1}{16}$ | B. | $\frac{1}{64}$ | C. | $\frac{1}{128}$ | D. | $\frac{1}{256}$ |
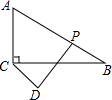 如图,在Rt△ABC中.∠ACB=90°,∠B=30°,CB=3$\sqrt{3}$,点D是平面上一点且CD=2,点P为线段AB上一动点.当△ABC绕点C任意旋转时,在旋转过程中线段DP长度的最大值为2+3$\sqrt{3}$,最小值为$\frac{3\sqrt{3}}{2}$-2.
如图,在Rt△ABC中.∠ACB=90°,∠B=30°,CB=3$\sqrt{3}$,点D是平面上一点且CD=2,点P为线段AB上一动点.当△ABC绕点C任意旋转时,在旋转过程中线段DP长度的最大值为2+3$\sqrt{3}$,最小值为$\frac{3\sqrt{3}}{2}$-2. 已知数a、b、c在数轴上的位置如图所示,化简|a+b|-|a-b|+|a+c|=a-c.
已知数a、b、c在数轴上的位置如图所示,化简|a+b|-|a-b|+|a+c|=a-c.