题目内容
17.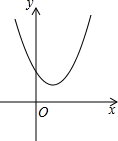 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(0,3),且当x=1时,y有最小值2.
如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(0,3),且当x=1时,y有最小值2.(1)求a,b,c的值;
(2)设二次函数y=k(2x+2)-(ax2+bx+c)(k为实数),它的图象的顶点为D.
①当k=1时,求二次函数y=k(2x+2)-(ax2+bx+c)的图象与x轴的交点坐标;
②请在二次函数y=ax2+bx+c与y=k(2x+2)-(ax2+bx+c)的图象上各找出一个点M,N,不论k取何值,这两个点始终关于x轴对称,直接写出点M,N的坐标(点M在点N的上方);
③过点M的一次函数y=-$\frac{3}{4}$x+t的图象与二次函数y=ax2+bx+c的图象交于另一点P,当k为何值时,点D在∠NMP的平分线上?
④当k取-2,-1,0,1,2时,通过计算,得到对应的抛物线y=k(2x+2)-(ax2+bx+c)的顶点分别为(-1,-6,),(0,-5),(1,-2),(2,3),(3,10),请问:顶点的横、纵坐标是变量吗?纵坐标是如何随横坐标的变化而变化的?
分析 (1)利用顶点式的解析式求解即可;
(2))①当k=1时,y=-x2+4x-1,令y=0,-x2+4x-1=0,解得x的值,即可得出图象与x轴的交点坐标;
②y=k(2x+2)-(ax2+bx+c)当经x=-1时,y=ax2+bx+c与y=k(2x+2)-(ax2+bx+c)的图象上点M,N,不论k取何值,这两个点始终关于x轴对称,可得M(-1,6),N(-1,-6);
③由y=-$\frac{3}{4}$+t,经过(-1,6),可得t的值,由ME⊥x轴,可得E点的横坐标为-1,可得出AE,ME,MA的值.设MD交AE于点B,作BC⊥AM于点C,设BC=x,则AB=8-x,显然△ABC∽△AMN,可求出x的值,即可得出MD的函数表达式为y=-2x+4.再把点D代入,即可求出k的值;
④观察可得出当顶点的横坐标大于-1时,纵坐标随横坐标的增大而增大,当顶点的横坐标小于-1时,纵坐标随横坐标的增大而减小.
解答 解:(1)设y=a(x-1)2+2,将(0,3)代入,得a=1,
∴y=(x-1)2+2,即y=x2-2x+3,
∴a=1,b=-2,c=3;
(2)①当k=1时,y=-x2+4x-1,令y=0,-x2+4x-1=0,解得x=2±$\sqrt{3}$,即图象与x轴的交点坐标(2+$\sqrt{3}$,0),(2-$\sqrt{3}$,0);
②y=k(2x+2)-(ax2+bx+c)当经x=-1时,y=ax2+bx+c与y=k(2x+2)-(ax2+bx+c)的图象上点M,N,不论k取何值,这两个点始终关于x轴对称,
∴M(-1,6),N(-1,-6),
③y=-$\frac{3}{4}$x+t,经过(-1,6),得t=$\frac{21}{4}$,
∴y=-$\frac{3}{4}$x+$\frac{21}{4}$,则A(7,0),
∵ME⊥x轴,
∴E点的横坐标为-1,
∴AE=8,
∵ME=6,
∴MA=10.
如图1,设MD交AE于点B,作BC⊥AM于点C,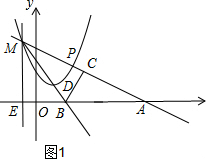
∵MD平分∠NMP,ME⊥x轴,
∴BC=BE,设BC=x,则AB=8-x,显然△ABC∽△AME,
∴$\frac{x}{8-x}$=$\frac{3}{5}$,则x=3.得点B(2,0),
∴MD的函数表达式为y=-2x+4.
∵y=ax2+bx+c与y=k(2x+2)-(ax2+bx+c)=-[x-(k+1)]2+(k+1)2+2k-3.
把D(k+1,k2+2k+1+2k-3),代入y=-2x+4.得k=-3±$\sqrt{13}$,
由y=k(2x+2)-(ax2+bx+c)有意义可得k=-3+$\sqrt{13}$,
④是.
当顶点的横坐标大于-1时,纵坐标随横坐标的增大而增大,
当顶点的横坐标小于-1时,纵坐标随横坐标的增大而减小.
点评 本题主要考查了二次函数,涉及二次函数的解析式的求法,一次函数的知识及相似三角形,解题的关键是把二次函数图象与其它函数图象相结合解决问题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | 4 | D. | -4 |
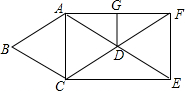 如图,在菱形ABCD中,∠B=60°,AB=1,延长AD到点E,使DE=AD,延长CD到点F,使DF=CD,连接AC、CE、EF、AF,则下列描述正确的是( )
如图,在菱形ABCD中,∠B=60°,AB=1,延长AD到点E,使DE=AD,延长CD到点F,使DF=CD,连接AC、CE、EF、AF,则下列描述正确的是( )| A. | 四边形ACEF是平行四边形,它的周长是4 | |
| B. | 四边形ACEF是矩形,它的周长是2+2$\sqrt{3}$ | |
| C. | 四边形ACEF是平行四边形,它的周长是4$\sqrt{3}$ | |
| D. | 四边形ACEF是矩形,它的周长是4+4$\sqrt{3}$ |
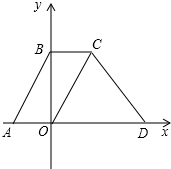 如图,在平面直角坐标系中,点O为坐标原点,直线y=2x+4交X轴于点A,交y轴于点B,四边形ABCO是平行四边形,直线y=-x+m经过点C,交x轴于点D.
如图,在平面直角坐标系中,点O为坐标原点,直线y=2x+4交X轴于点A,交y轴于点B,四边形ABCO是平行四边形,直线y=-x+m经过点C,交x轴于点D.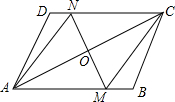 如图,在?ABCD中,点O是对角线AC的中点,过点O的直线MN分别交AB、CD于点M、N,连结AN,CM.
如图,在?ABCD中,点O是对角线AC的中点,过点O的直线MN分别交AB、CD于点M、N,连结AN,CM. 数轴上实数b的对应点的位置如图所示,比较大小:$\frac{1}{2}$b+1>0.
数轴上实数b的对应点的位置如图所示,比较大小:$\frac{1}{2}$b+1>0.