Question

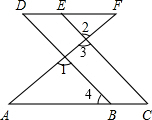
认真阅读并填空
已知：如图，∠1=∠2，∠C=∠D，试说明：∠A=∠F
解：∵∠1=∠2（已知），∠2=∠3（

 

）
∴∠1=∠3（等量代换）
∴BD∥EC（

 

）
∴∠4=∠C（两直线平行，同位角相等）
又∵∠C=∠D（已知）
∴∠4=∠D（

 

）
∴AC∥DF（内错角相等，两直线平行）
∴∠A=∠F（

 

）

Answer 1

考点：平行线的判定与性质

专题：推理填空题

分析：求出∠1=∠3，根据平行线的判定推出BD∥EC，根据平行线的性质和已知求出∠4=∠D，推出AC∥DF，根据平行线的性质推出即可．

解答：解：∵∠1=∠2（已知），∠2=∠3（对顶角相等），
∴∠1=∠3（等量代换），
∴BD∥EC（同位角相等，两直线平行），
∴∠4=∠C（两直线平行，同位角相等）
又∵∠C=∠D（已知）
∴∠4=∠D（等量代换），
∴AC∥DF（内错角相等，两直线平行）
∴∠A=∠F（两直线平行，内错角相等），
故答案为：对顶角相等，同位角相等，两直线平行，等量代换，两直线平行，内错角相等．

点评：本题考查了平行线的性质和判定的应用，主要考查学生运用平行线的判定和性质进行推理的能力，难度适中．