题目内容
20.已知二次函数y=-$\frac{1}{2}$x2+x+4.(1)求抛物线的顶点坐标和对称轴;
(2)当x取何值时,y随x的增大而增大?当x取何值时,y随x的增大而减小?当x取何值时,y有最大值还是最小值?是多少?
分析 (1)根据函数解析式可求出顶点坐标,对称轴及与坐标轴的交点;
(2)根据确定的对称轴及顶点坐标确定其增减性即可.
解答 解:(1)∵y=-$\frac{1}{2}$x2+x+4=-$\frac{1}{2}$(x2-2x+1-1)+4=-$\frac{1}{2}$(x-1)2+$\frac{9}{2}$,
∴顶点坐标为(1,$\frac{9}{2}$),对称轴为x=1;
(2)∵开口向下且对称轴为x=1,
∴当x<1时,y随x的增大而增大;当x>1时y随x的增大而减小;
函数有最大值为$\frac{9}{2}$.
点评 本题考查了二次函数的性质,解题的关键是能够确定函数的对称轴及顶点坐标.

练习册系列答案
相关题目
8.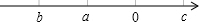 如果实数a,b,c在数轴上的位置如图所示,那么代数式$\sqrt{{a}^{2}}$+|b-a|+$\sqrt{(b+c)^{2}}$可以化简为( )
如果实数a,b,c在数轴上的位置如图所示,那么代数式$\sqrt{{a}^{2}}$+|b-a|+$\sqrt{(b+c)^{2}}$可以化简为( )
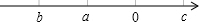 如果实数a,b,c在数轴上的位置如图所示,那么代数式$\sqrt{{a}^{2}}$+|b-a|+$\sqrt{(b+c)^{2}}$可以化简为( )
如果实数a,b,c在数轴上的位置如图所示,那么代数式$\sqrt{{a}^{2}}$+|b-a|+$\sqrt{(b+c)^{2}}$可以化简为( )| A. | -c-2b | B. | a-2b-c | C. | -2a-c | D. | c |
12.李明的家在汽车站(O)的东偏北18°方向500米的A处,学校B在汽车站(O)的南偏西10°方向600米处,李明上学经汽车站所走的角∠AOB=( )
| A. | 28° | B. | 108° | C. | 118° | D. | 98° |
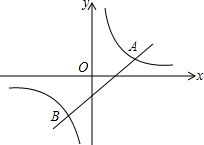 如图,直线y=$\frac{1}{2}$x-3+b与双曲线y=$\frac{1}{x}$交于A,B两点,则线段AB长度的最小值是$\sqrt{10}$.
如图,直线y=$\frac{1}{2}$x-3+b与双曲线y=$\frac{1}{x}$交于A,B两点,则线段AB长度的最小值是$\sqrt{10}$.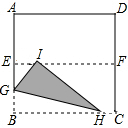 如图,将边长为4的正方形ABCD对折后展开,折痕为EF,分别在边AB、BC上取点G、H,沿GH对折,使点B落在折痕EF上,落点记为I,则:
如图,将边长为4的正方形ABCD对折后展开,折痕为EF,分别在边AB、BC上取点G、H,沿GH对折,使点B落在折痕EF上,落点记为I,则: