题目内容
11.△ABC是等边三角形,AB=4cm,则BC边上的高AD=2$\sqrt{3}$.分析 根据等边三角形的性质可求得∠BAD=30°,已知AB=4,则在RT△ABD中,可得到BD的长,再利用勾股定理求得AD的长.
解答 解:∵△ABC是等边三角形,AD是BC边上的高,
∴∠BAD=30°,
在Rt△ABC中,AB=4,
∴BD=2,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
故答案为2$\sqrt{3}$.
点评 此题主要考查了等边三角形的性质,关键是掌握等腰三角形底边上的中线和底边上的高,以及顶角的平分线重合.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
6.服装店销售某款服装,一件服装的标价为300元,若按标价的八折销售,仍可获利60元,则这款服装每件的进价为( )
| A. | 60元 | B. | 80元 | C. | 120元 | D. | 180元 |
1.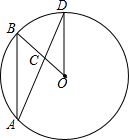 如图所示,在⊙O中,∠BOD=30°,OD∥AB,AD,OB相交于点C,那么∠BCD的度数是( )
如图所示,在⊙O中,∠BOD=30°,OD∥AB,AD,OB相交于点C,那么∠BCD的度数是( )
 如图所示,在⊙O中,∠BOD=30°,OD∥AB,AD,OB相交于点C,那么∠BCD的度数是( )
如图所示,在⊙O中,∠BOD=30°,OD∥AB,AD,OB相交于点C,那么∠BCD的度数是( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
 如图,已知函数y1=3x+b和y2=ax-3的图象交于点P(-2,-5),则不等式3x+b>ax-3的解集为x>-2.
如图,已知函数y1=3x+b和y2=ax-3的图象交于点P(-2,-5),则不等式3x+b>ax-3的解集为x>-2.