题目内容
19.已知抛物线y=$\frac{1}{5}$(x-5)2的顶点为A,抛物线与y轴交于点B,过点B作x轴的平行线交抛物线于另外一点C.(1)求A,B,C三点的坐标;
(2)求△ABC的面积;
(3)试判断△ABC的形状并说明理由.
分析 (1)利用顶点式直接得出顶点坐标A即可,另x=0,得出与y轴交点B,利用对称性的出过点B作x轴的平行线交抛物线于另外一点C;
(2)利用三角形的面积计算公式求得答案即可;
(3)分别求得AB、BC、AC,进一步利用勾股定理逆定理判定即可.
解答 解:如图,
(1)抛物线y=$\frac{1}{5}$(x-5)2的顶点为A(5,0),
由x=0,则y=5,抛物线与y轴交,点B为(0,5),
因为对称轴为直线x=5,所以点C的坐标为(10,5);
(2)S△ABC=$\frac{1}{2}$×10×5=25;
(3)AB=AC=5$\sqrt{2}$,BC=10,
∵AB2+AC2=BC2,
∴△ABC是等腰直角三角形.
点评 此题考查二次函数的性质,三角形的面积,勾股定理与勾股定理逆定理的运用,利用二次函数的对称性是解决问题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 如图,在矩形ABCD中,E是边CD的中点.BF⊥AE.垂足为点F.设AB=a,BC=b,求BF的长.
如图,在矩形ABCD中,E是边CD的中点.BF⊥AE.垂足为点F.设AB=a,BC=b,求BF的长.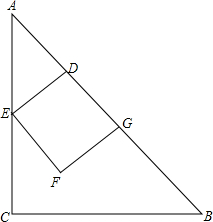 如图,在Rt△ABC中,∠ACB=90°,CA=CB=6,动点D从点A出发沿AB以每秒$\sqrt{2}$个单位的速度向点B运动,到达点B时停止运动,过点D作AB的垂线交折线AC-BC于点E,以DE为边向下作正方形DEFG,点G在AB上,正方形DEFG与△ABC重叠部分的面积为y,动点D运动的时间为t.
如图,在Rt△ABC中,∠ACB=90°,CA=CB=6,动点D从点A出发沿AB以每秒$\sqrt{2}$个单位的速度向点B运动,到达点B时停止运动,过点D作AB的垂线交折线AC-BC于点E,以DE为边向下作正方形DEFG,点G在AB上,正方形DEFG与△ABC重叠部分的面积为y,动点D运动的时间为t.