题目内容
某水果批发商经销一种高档水果,如果每千克盈利10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?
(Ⅰ)设每千克应涨价x元,根据问题中的数量关系,用含x的代数式填表:
(Ⅱ)列出方程,并求问题的解.
(Ⅰ)设每千克应涨价x元,根据问题中的数量关系,用含x的代数式填表:
| 每千克盈利(元) | 每天销售量(千克) | 每天盈利(元) | |
| 涨价前 | 10 | 500 | 5000 |
| 涨价后 | 6000 |
考点:一元二次方程的应用
专题:销售问题
分析:(1)根据涨的价格+原来的盈利=现在的盈利,原来的销量-减少的销量就可以求出结论;
(2)设每千克应涨价x元,则现在的利润为(x+10)元,销量为(500-20x),由总利润=每个利润×数量建立方程求出其解即可.
(2)设每千克应涨价x元,则现在的利润为(x+10)元,销量为(500-20x),由总利润=每个利润×数量建立方程求出其解即可.
解答:解:(1)由题意,得
涨价后的盈利为:(10+x)元,每天的销量为:(500-20x)千克;
故答案为:10+x,500-20x
(2)设每千克应涨价x元,则现在的利润为(x+10)元,销量为(500-20x),由题意,得
(10+x)(500-20x)=6000.
解得:x1=5,x2=10.
∵要使顾客得到实惠,
∴x=5.
答:每千克应涨价5元.
涨价后的盈利为:(10+x)元,每天的销量为:(500-20x)千克;
故答案为:10+x,500-20x
(2)设每千克应涨价x元,则现在的利润为(x+10)元,销量为(500-20x),由题意,得
(10+x)(500-20x)=6000.
解得:x1=5,x2=10.
∵要使顾客得到实惠,
∴x=5.
答:每千克应涨价5元.
点评:本题考查了代数式表示数的运用,列一元二次方程解实际问题的运用,销售问题的数量关系的运用,解答时由销售问题的数量关系建立方程是关键.

练习册系列答案
相关题目
下列说法正确的是( )
| A、打开电视机,正在播新闻是必然事件 |
| B、甲组数据的方差S甲2=0.24,乙组数据的方差S乙2=0.03,则乙组数据比甲组数据稳定 |
| C、一组数据2,4,5,5,3,6的平均数5 |
| D、掷一枚硬币一定正面朝上 |
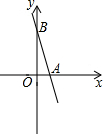 已知:如图,在平面直角坐标系xOy中,一次函数y=-4x+8的图象分别与x、y轴交于点A、B,点P在x轴的负半轴上,△ABP的面积为12.若一次函数y=kx+b的图象经过点P和点B,求这个一次函数y=kx+b表达式.
已知:如图,在平面直角坐标系xOy中,一次函数y=-4x+8的图象分别与x、y轴交于点A、B,点P在x轴的负半轴上,△ABP的面积为12.若一次函数y=kx+b的图象经过点P和点B,求这个一次函数y=kx+b表达式. 如图,⊙O的直径为10cm,弦AB=8cm,P是弦AB上的一个动点,求OP的长度范围.
如图,⊙O的直径为10cm,弦AB=8cm,P是弦AB上的一个动点,求OP的长度范围.
 如图,△ABC与△DCB中,AC与BD交于点E,且∠ABC=∠DCB,AB=DC.
如图,△ABC与△DCB中,AC与BD交于点E,且∠ABC=∠DCB,AB=DC. 某体育用品商店试销一款成本为50元的排球,规定试销期间单价不低于成本价,且获利不得高于40%.经试销发现,销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系.
某体育用品商店试销一款成本为50元的排球,规定试销期间单价不低于成本价,且获利不得高于40%.经试销发现,销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系.