题目内容
19.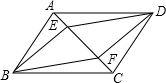 如图,在平行四边形ABCD中,对角线AC上有E、F两点,要使四边形BEDF是平行四边形,还需要增加一个条件是AE=CF.(填上一个即可).
如图,在平行四边形ABCD中,对角线AC上有E、F两点,要使四边形BEDF是平行四边形,还需要增加一个条件是AE=CF.(填上一个即可).
分析 连接BD交AC于点O,由平行四边形的性质可得到OB=OD,要证明四边形BEDF为平行四边形,只需要OE=OF即可,故添加的条件只要能证明OE=OF即可.
解答 解:
如图,连接BD交AC于点O,
∵四边形ABCD为平行四边形,
∴OB=OD,OA=OC,
若AE=CF,则有AO-AE=CO-CF,即OE=OF,
∴四边形BEDF为平行四边形,
故答案为:AE=CF.
点评 本题主要考查平行四边形的判定,掌握平行四边形的判定方法是解题的关键.即①两组对边分别平行的四边形是平行四边形,②两组对边分别相等的四边形是平行四边形,③一组对边平行且相等的四边形是平行四边形,④两组对角分别相等的四边形是平行四边形,⑤对角线互相平分的四边形是平行四边形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.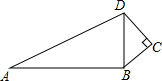 如图,己知∠C=90°,AB=12,BC=3,CD=4,∠ABD=90°,则AD=( )
如图,己知∠C=90°,AB=12,BC=3,CD=4,∠ABD=90°,则AD=( )
 如图,己知∠C=90°,AB=12,BC=3,CD=4,∠ABD=90°,则AD=( )
如图,己知∠C=90°,AB=12,BC=3,CD=4,∠ABD=90°,则AD=( )| A. | 10 | B. | 13 | C. | 8 | D. | 11 |
14.下列说法正确的是( )
| A. | 顺次连接矩形各边中点的四边形一定也是矩形 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 有一个角是直角的菱形一定是正方形 | |
| D. | 平行四边形的对角线相等且互相平分 |
8.若一个菱形的两条对角线长分别是5cm和10cm,则与该菱形面积相等的正方形的边长是( )
| A. | 6cm | B. | 5cm | C. | $\sqrt{5}$cm | D. | 7.5cm |
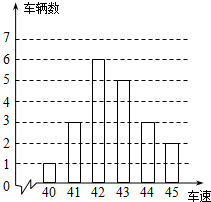 如图是交警在某个路口统计的某时段来往车辆的车速情况.(单位:千米/时).
如图是交警在某个路口统计的某时段来往车辆的车速情况.(单位:千米/时).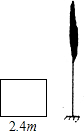 国旗法对国旗的构成由明确的规定,国旗应为长方形,长与宽的比为3:2,某学校所使用的国旗正是按这一比例制作的,长为2.4m.已知学校的旗杆高为10m,在无风的天气里,国旗会自然下垂,求国旗下垂时最低处离地面的距离是多少?(结果保留一位小数,$\sqrt{13}$≈3.6)
国旗法对国旗的构成由明确的规定,国旗应为长方形,长与宽的比为3:2,某学校所使用的国旗正是按这一比例制作的,长为2.4m.已知学校的旗杆高为10m,在无风的天气里,国旗会自然下垂,求国旗下垂时最低处离地面的距离是多少?(结果保留一位小数,$\sqrt{13}$≈3.6)