题目内容
3.已知等腰三角形两边长分别为6和10,则底角的余弦值为$\frac{\sqrt{11}}{6}$或$\frac{\sqrt{91}}{10}$.分析 分腰长为6,底边长10和腰长为10,底边长6两种情况,根据等腰三角形的性质、勾股定理、余弦的概念计算即可.
解答 解:①当等腰三角形ABC的腰长为6,底边长10时,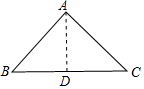
作底边BC的高AD,
则BD=CD=5,
由勾股定理得,AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{11}$,
在Rt△ADB中,cosB=$\frac{AD}{AB}$=$\frac{\sqrt{11}}{6}$,
②当等腰三角形ABC的腰长为10,底边长6时,
BD=CD=3,
由勾股定理得,AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{91}$,
在Rt△ADB中,cosB=$\frac{AD}{AB}$=$\frac{\sqrt{91}}{10}$,
故答案为:$\frac{\sqrt{11}}{6}$或$\frac{\sqrt{91}}{10}$.
点评 本题考查的是等腰三角形的性质、余弦的概念,掌握等腰三角形的三线合一、勾股定理的应用、余弦的概念是解题的关键,注意分情况讨论思想的运用.

练习册系列答案
相关题目
8.我市为了增强学生的体质,组织了一次排球联赛,赛制为单循环形式(每两队之间都赛一场),共进行了15场比赛,则参加比赛的球队共有( )
| A. | 4个 | B. | 5个 | C. | 6个 | D. | 5个或6个 |
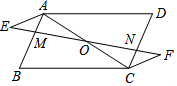 如图,四边形ABCD中,AB∥CD,BC∥DA,过AC的中点O作一条直线分别与AB、CD交于点M、N,点E、F在直线MN上,且OE=OF.
如图,四边形ABCD中,AB∥CD,BC∥DA,过AC的中点O作一条直线分别与AB、CD交于点M、N,点E、F在直线MN上,且OE=OF. 如图,矩形ABCD中,AB=4,AD=3,把矩形ABCD沿对角线AC折叠,使点B落在点E处,AE交CD于点F,连接DE
如图,矩形ABCD中,AB=4,AD=3,把矩形ABCD沿对角线AC折叠,使点B落在点E处,AE交CD于点F,连接DE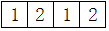 由若干个相同的小正方体搭成的一个几何体的俯视图如图所示,小正方形中的数字表示该位置的小正方体的个数,这个几何体的主视图是( )
由若干个相同的小正方体搭成的一个几何体的俯视图如图所示,小正方形中的数字表示该位置的小正方体的个数,这个几何体的主视图是( )