Question

如图，已知：△ABC中，AB=AC，∠BAC=90°，分别过B，C向经过点A的直线EF作垂线，垂足为E，F．

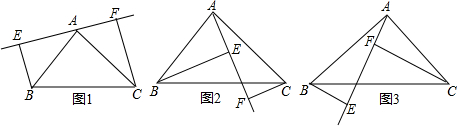
（1）当EF与斜边BC不相交时，请证明EF=BE+CF（如图1）；
（2）如图2，当EF与斜边BC这样相交时，其他条件不变，证明：EF=BE-CF；
（3）如图3，当EF与斜边BC这样相交时，猜想EF、BE、CF之间的关系，不必证明．

Answer 1

考点：全等三角形的判定与性质,等腰直角三角形

专题：几何综合题,探究型

分析：（1）求出△BEA≌△AFC，推出EA=FC，BE=AF，即可得出答案；
（2）求出△BEA≌△AFC，推出EA=FC，BE=AF，即可得出答案；
（3）求出△BEA≌△AFC，推出EA=FC，BE=AF，即可得出答案．

解答：（1）证明：∵BE⊥EA，CF⊥AF，
∴∠BAC=∠BEA=∠CFE=90°，
∴∠EAB+∠CAF=90°，∠EBA+∠EAB=90°，
∴∠CAF=∠EBA，
在△ABE和△CAF中，

∠BEA=∠AFC ∠EBA=∠FAC AB=AC

∴△BEA≌△AFC，
∴EA=FC，BE=AF，
∴EF=EA+AF=BE+CF．

（2）证明：∵BE⊥EA，CF⊥AF，
∴∠BAC=∠BEA=∠CFE=90°，
∴∠EAB+∠CAF=90°，∠ABE+∠EAB=90°，
∴∠CAF=∠ABE，
在△ABE和△ACF中，

∠EBA=∠FAC ∠BEA=∠CFA AB=AC

∴△BEA≌△AFC，
∴EA=FC，BE=AF，
∵EF=AF-AE，
∴EF=BE-CF．

（3）EF=CF-BE，
理由是：：∵BE⊥EA，CF⊥AF，
∴∠BAC=∠BEA=∠CFA=90°，
∴∠EAB+∠CAF=90°，∠ABE+∠EAB=90°，
∴∠CAF=∠ABE，
在△ABE和△ACF中，

∠EBA=∠FAC ∠BEA=∠CFA AB=AC

∴△BEA≌△AFC，
∴EA=FC，BE=CF，
∵EF=EA-AF，
∴EF=CF-BE．

点评：本题考查了全等三角形的性质和判定的应用，题目具有一定的代表性，是一道比较好的题目，证明过程类似．