题目内容
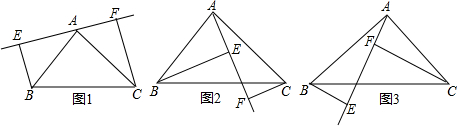
 如图,在△ABC中,AB=AC,D是BC上任一点,且2AD2=BD2+CD2.求证:△ABC是直角三角形.
如图,在△ABC中,AB=AC,D是BC上任一点,且2AD2=BD2+CD2.求证:△ABC是直角三角形.考点:勾股定理
专题:证明题
分析:作AE⊥BC于E,由于AB=AC,所以BE=CE,由勾股定理可得出AD2=AE2+ED2,BD=ED+BE,CD=CE-DE,代入2AD2=BD2+CD2求出AE=BE=CE三者之间的关系,得到∴△AEB与△AEC都是等腰直角三角形,即可得证.
解答: 证明:作AE⊥BC于E,如图所示:
证明:作AE⊥BC于E,如图所示:
由题意得:ED=BD-BE=CE-CD,
∵在△ABC中,AB=AC,
∴BE=CE,
由勾股定理可得:
AD2=AE2+DE2,
∵BD2+CD2=(BE+ED)2+(CE-DE)2=BE2+CE2+2DE2,
∵2AD2=BD2+CD2,
∴2AE2+2DE2=BE2+CE2+2DE2,
∴2AE2=BE2+CE2,
∴AE=BE=CE,
∴△AEB与△AEC都是等腰直角三角形,
∴∠BAE=∠CAE=45°,
∴∠BAC=90°,
∴△ABC是直角三角形.
 证明:作AE⊥BC于E,如图所示:
证明:作AE⊥BC于E,如图所示:由题意得:ED=BD-BE=CE-CD,
∵在△ABC中,AB=AC,
∴BE=CE,
由勾股定理可得:
AD2=AE2+DE2,
∵BD2+CD2=(BE+ED)2+(CE-DE)2=BE2+CE2+2DE2,
∵2AD2=BD2+CD2,
∴2AE2+2DE2=BE2+CE2+2DE2,
∴2AE2=BE2+CE2,
∴AE=BE=CE,
∴△AEB与△AEC都是等腰直角三角形,
∴∠BAE=∠CAE=45°,
∴∠BAC=90°,
∴△ABC是直角三角形.
点评:本题主要考查勾股定理,关键在于找出直角三角形利用勾股定理求证,本题主要运用“等量代换”求出BE、CE、AE三者之间的关系.

练习册系列答案
相关题目